1 1 2 3 4 5
News Co
May 08, 2025 · 5 min read
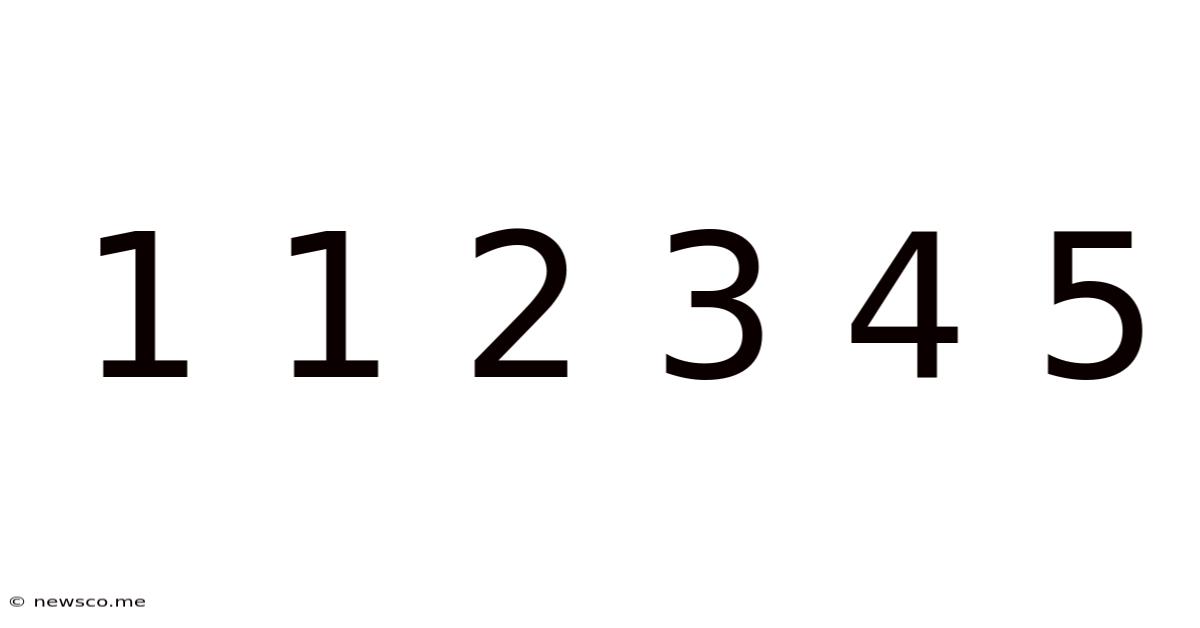
Table of Contents
Decoding the Sequence: 1 1 2 3 4 5 – A Deep Dive into Patterns, Possibilities, and Practical Applications
The seemingly simple sequence "1 1 2 3 4 5" might initially appear unremarkable. However, a closer examination reveals a wealth of potential interpretations, mathematical patterns, and even practical applications across various fields. This article will delve into the depths of this intriguing sequence, exploring its inherent structure, uncovering hidden patterns, and showcasing its surprising relevance in diverse contexts.
Understanding the Sequence's Intrinsic Nature
At first glance, the sequence "1 1 2 3 4 5" appears straightforward – a simple ascending series of natural numbers. However, this perception is superficial. The repetition of "1" at the beginning immediately introduces an element of intrigue. This repetition challenges the assumption of a strictly linear progression. Is it a coincidence, or does this repetition hold a key to unlocking a deeper understanding of the sequence's underlying structure?
The Potential for Multiple Interpretations
The beauty of this sequence lies in its inherent ambiguity. It lacks a single, definitive interpretation. This open-endedness allows for diverse approaches to analysis and fosters creative exploration. We can approach it from several angles:
-
As a purely numerical sequence: This perspective focuses on the raw numerical values and seeks patterns based on mathematical operations. We can analyze differences between consecutive terms, look for ratios, or explore potential connections to established mathematical series.
-
As a symbolic sequence: This approach considers the numbers not merely as numerical values but as symbols, potentially representing concepts or quantities within a specific context. The interpretation would depend on the assigned meaning to each number.
-
As a foundational sequence for a larger pattern: It is possible that "1 1 2 3 4 5" is a truncated version of a longer sequence, a subsequence within a more complex pattern. Extrapolating the sequence and searching for similar patterns in mathematical series could help reveal its true nature.
Exploring Mathematical Patterns within the Sequence
Let's delve into the mathematical possibilities:
1. Differences between Consecutive Terms
Analyzing the differences between consecutive terms can reveal underlying patterns.
- 1 - 1 = 0
- 2 - 1 = 1
- 3 - 2 = 1
- 4 - 3 = 1
- 5 - 4 = 1
This reveals a pattern where the differences, after the initial 0, become a constant sequence of 1s. This suggests a linear progression, at least from the second term onwards.
2. Searching for Ratios
Examining the ratios between consecutive terms doesn't reveal a consistent pattern in this short sequence. However, extending the sequence might unveil ratios that provide further insights.
3. Fibonacci-like Sequences and Variations
While not a perfect Fibonacci sequence (where each number is the sum of the two preceding ones), the sequence shares similarities. This suggests the potential for a related, generalized Fibonacci sequence or a variation where the initial conditions are modified.
4. Exploring Polynomial Relationships
It's possible to fit a polynomial function to the sequence, potentially revealing a formula that generates each term. While multiple polynomials could fit the limited data, finding a low-degree polynomial that fits the sequence and can be extrapolated to generate future terms could be insightful.
Expanding the Sequence: Exploring Potential Extrapolations
The limited length of the sequence prevents definitive conclusions. To gain deeper insights, let's explore potential extrapolations:
1. Simple Linear Extrapolation
The simplest extrapolation would be to continue the linear progression: 1 1 2 3 4 5 6 7 8... This is a straightforward approach but might overlook more intricate patterns.
2. Extrapolation based on Differences
Considering the differences between consecutive terms, the next term would be 5 + 1 = 6, followed by 7, 8, and so on. This reinforces the possibility of a linear progression.
3. Exploring more complex extrapolations
More sophisticated extrapolations could involve searching for patterns in higher-order differences or exploring connections to other mathematical sequences. This would require a more advanced mathematical approach and might involve iterative processes or algorithmic analysis.
Practical Applications and Interpretations
While seemingly abstract, the sequence "1 1 2 3 4 5" could have practical applications in various fields. Here are a few examples:
1. Coding and Programming
The sequence could represent a simplified form of data or a starting point for an algorithm. It could serve as an example for demonstrating basic programming concepts such as loops, arrays, or sequence generation.
2. Data Analysis and Modeling
In data analysis, the sequence could be a simplified representation of a time series or a part of a larger dataset. Analyzing its patterns could provide insights into potential underlying trends or anomalies.
3. Cryptography and Security
Although simplistic, the sequence could serve as a rudimentary example in cryptography, showing how patterns can be used to encode or decode simple messages. While not secure for real-world applications, it provides a foundational illustration of cryptographic principles.
4. Game Theory and Strategy
The sequence, if embedded within a game context, could represent game states, scores, or progression levels. Its interpretation would then be highly dependent on the specific rules and structure of the game.
5. Combinatorics and Probability
Depending on the context, the sequence might represent certain combinatorial arrangements or probabilities. Further exploration would be required to identify specific applications in this field.
Conclusion: The Enduring Mystery and Potential of 1 1 2 3 4 5
The sequence "1 1 2 3 4 5," while initially appearing trivial, proves to be surprisingly rich in potential interpretations and mathematical explorations. Its inherent ambiguity opens doors to diverse approaches, fostering creativity and deepening our understanding of mathematical patterns and their practical applications. Whether viewed as a simple numerical sequence, a symbolic representation, or a fragment of a larger, more complex pattern, this sequence encourages critical thinking and reveals the potential for unexpected discoveries within the seemingly mundane. Further research, particularly with extended versions of the sequence or within specific contextual applications, could potentially unveil even more fascinating insights. The enduring mystery of this simple sequence encourages us to continually explore and question the nature of mathematical patterns and their profound implications in various aspects of our lives.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 3 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.