1 1 2 3 5 9
News Co
May 08, 2025 · 5 min read
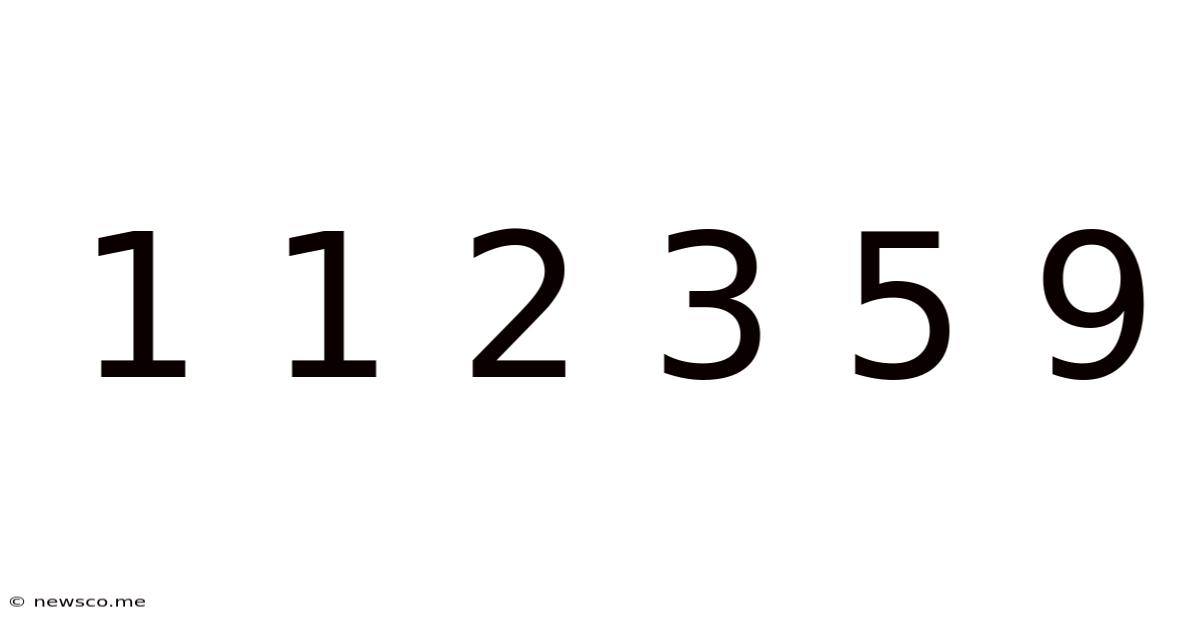
Table of Contents
- 1 1 2 3 5 9
- Table of Contents
- Decoding the Mystery: Exploring the Sequence 1, 1, 2, 3, 5, 9...
- Understanding the Sequence: A Recursive Journey
- Connections to the Fibonacci Sequence: A Family Resemblance
- Exploring Mathematical Properties: Unveiling the Secrets
- Applications in Programming and Algorithms: Practical Implementations
- Beyond the Numbers: A Deeper Dive into Mathematical Patterns
- Further Exploration and Research: Unanswered Questions
- Conclusion: A Sequence with Enduring Appeal
- Latest Posts
- Related Post
Decoding the Mystery: Exploring the Sequence 1, 1, 2, 3, 5, 9...
The seemingly simple sequence 1, 1, 2, 3, 5, 9... might appear innocuous at first glance. However, beneath its unassuming exterior lies a fascinating mathematical puzzle that has captivated minds for centuries. This sequence, a variation on the Fibonacci sequence, unveils deeper connections to nature, programming, and various mathematical concepts. Let's delve into the intriguing world of this number pattern, exploring its generation, its properties, and its surprising applications.
Understanding the Sequence: A Recursive Journey
The core of understanding this sequence lies in recognizing its recursive nature. Unlike an arithmetic or geometric sequence with a constant difference or ratio, this sequence defines each term as a function of the preceding terms. The pattern is not immediately obvious, but it becomes clear with further investigation:
-
The first two terms are 1 and 1. This is our starting point. This sets the foundation for the entire sequence.
-
Each subsequent term is the sum of the three preceding terms. This recursive relationship is the key to generating the entire sequence. For example:
- 2 = 1 + 1 (the sum of the first two terms)
- 3 = 1 + 1 + 1 (the sum of the first three terms)
- 5 = 1 + 2 + 2 (the sum of the three preceding terms)
- 9 = 2 + 3 + 4 (the sum of the three preceding terms)
This recursive definition allows us to extend the sequence indefinitely. We can continue to generate more terms: 14, 23, 37, 60, 97, and so on. The elegance of this method lies in its simplicity and its ability to create a seemingly complex pattern from a straightforward rule.
Connections to the Fibonacci Sequence: A Family Resemblance
While distinct in its definition, the 1, 1, 2, 3, 5, 9... sequence shares a family resemblance with the famous Fibonacci sequence (1, 1, 2, 3, 5, 8...). Both sequences exhibit a recursive structure, where each term depends on the preceding terms. However, the crucial difference lies in the number of preceding terms involved in the recursive relationship. The Fibonacci sequence adds only the two preceding terms, while our sequence sums the three preceding terms.
This subtle difference leads to distinct properties and applications. The Fibonacci sequence appears ubiquitously in nature, manifesting in the arrangement of leaves on a stem, the spiral pattern of sunflowers, and the branching of trees. While the 1, 1, 2, 3, 5, 9... sequence doesn't have such overtly obvious natural manifestations, its recursive structure highlights the underlying mathematical principles governing patterns in nature.
Exploring Mathematical Properties: Unveiling the Secrets
The sequence's recursive nature lends itself to several interesting mathematical properties. While a comprehensive mathematical analysis is beyond the scope of this blog post, we can explore some key aspects:
-
Growth Rate: Like the Fibonacci sequence, this sequence demonstrates exponential growth. The ratio between consecutive terms approaches a constant value as the sequence progresses. This constant is approximately 1.839, which is a root of the cubic equation x³ - x² - x - 1 = 0. This characteristic is a fundamental property of recursive sequences of this type.
-
Generating Functions: Mathematical tools like generating functions can provide a concise representation of the sequence. A generating function allows us to express the sequence as a power series, making it easier to analyze and manipulate. The specific generating function for this sequence is a more advanced mathematical concept requiring deeper exploration into generating functions theory.
-
Modulo Arithmetic: Exploring the sequence modulo various integers reveals cyclical patterns. Taking the remainder after division by a given number can reveal interesting repeating structures within the sequence. This opens up avenues for exploring number theory connections.
Applications in Programming and Algorithms: Practical Implementations
The recursive nature of the sequence makes it ideal for illustrating recursive programming techniques. Implementing the generation of this sequence in a programming language serves as a prime example for understanding and practicing recursion. It allows programmers to grasp the concepts of base cases and recursive calls.
Furthermore, the sequence, along with its variations, can inspire novel algorithms. While it might not be a direct component of widely used algorithms, its recursive structure can act as a foundation for developing new solutions in various computational domains, particularly where self-referential processes are involved.
Beyond the Numbers: A Deeper Dive into Mathematical Patterns
The 1, 1, 2, 3, 5, 9... sequence serves as a microcosm of the broader world of mathematical patterns. It demonstrates that seemingly simple numerical progressions can harbor complex and fascinating properties. The recursive structure, the connection to the Fibonacci sequence, and the potential for further mathematical exploration all contribute to the sequence's enduring appeal. It’s a testament to the elegance and power of mathematical relationships.
Further Exploration and Research: Unanswered Questions
The study of this sequence opens doors to a vast landscape of related mathematical concepts. Further research can focus on:
-
Generalizing the Sequence: Exploring sequences where the sum of n preceding terms is used to generate the next term. This opens up possibilities for understanding broader families of recursive sequences.
-
Closed-Form Expressions: While a recursive definition is sufficient, a closed-form expression (a formula that directly computes any term without computing previous terms) would provide a more efficient and insightful representation of the sequence. The search for such expressions can lead to valuable mathematical discoveries.
-
Connections to Other Mathematical Fields: Exploring potential links to areas like fractal geometry, chaos theory, or number theory might reveal unexpected connections and applications.
Conclusion: A Sequence with Enduring Appeal
The sequence 1, 1, 2, 3, 5, 9... offers a captivating journey into the world of mathematics. Its recursive nature, its relationship to the Fibonacci sequence, and its potential for further mathematical exploration make it a compelling subject for study. Whether you're a seasoned mathematician or a curious beginner, this seemingly simple sequence holds a wealth of intriguing possibilities waiting to be discovered. The simplicity of its generation belies its underlying mathematical richness, underscoring the beauty and power found within even the most basic numerical patterns. This sequence serves as a reminder that the world of mathematics is full of surprises, and the exploration of patterns, no matter how simple they appear, can lead to unexpected and rewarding discoveries.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 1 2 3 5 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.