1 1 2 4 3 9
News Co
Apr 23, 2025 · 5 min read
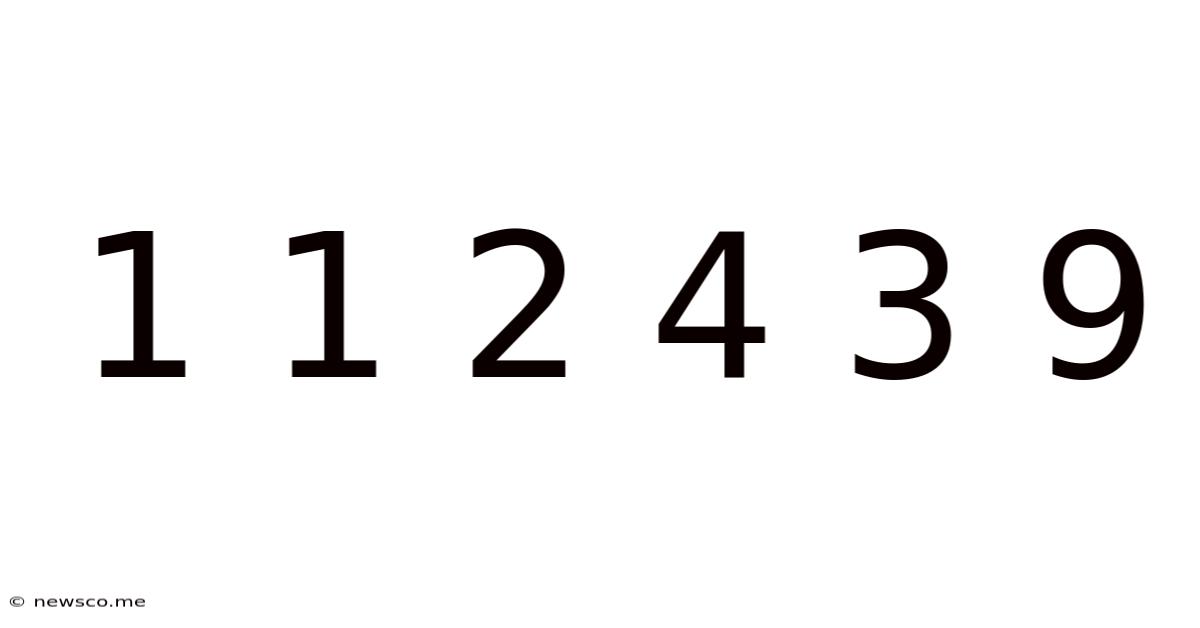
Table of Contents
Unlocking the Secrets of the Sequence: 1 1 2 4 3 9
The seemingly simple sequence, 1 1 2 4 3 9, presents a fascinating challenge for the mathematically inclined. At first glance, it appears random. Yet, a deeper dive reveals potential patterns and underlying structures, prompting us to explore various mathematical concepts and problem-solving approaches. This article will delve into the possibilities, exploring different perspectives on this intriguing number sequence and discussing the importance of pattern recognition and mathematical thinking.
The Allure of Pattern Recognition
The human brain is wired to seek patterns. This innate ability is crucial for survival, allowing us to predict events and make sense of the world around us. When confronted with a numerical sequence like 1 1 2 4 3 9, our minds instinctively search for a logical explanation, a rule that governs the progression of numbers. This inherent drive fuels our exploration of potential solutions and highlights the importance of pattern recognition in various fields, from mathematics and science to art and music. The quest to decipher this sequence is, in essence, a microcosm of this fundamental human characteristic.
Identifying Potential Patterns: A Multifaceted Approach
Several approaches can be used to decipher the sequence 1 1 2 4 3 9. The lack of an immediately obvious pattern makes this an exciting challenge. Let's explore some potential avenues:
-
Additive Patterns: Adding the previous two numbers doesn't yield a consistent result. Neither does adding consecutive numbers or any simple additive combination.
-
Multiplicative Patterns: Exploring multiplicative relationships is equally fruitless. There's no clear multiplier that consistently generates the next term.
-
Square Numbers: The numbers 1, 4, and 9 are all perfect squares (1², 2², 3²). However, the inclusion of 2 and 3 disrupts a straightforward perfect square pattern. This hints at a more complex relationship.
-
Fibonacci-like Sequences: While not a direct Fibonacci sequence (where each number is the sum of the two preceding ones), there's a possible link. The sequence shares a certain resemblance, but the deviations are significant enough to suggest a different underlying principle.
-
Polynomial Relationships: Could the sequence be generated by a polynomial function? This is a viable possibility, as a sufficiently complex polynomial could potentially fit the known terms. Finding such a polynomial would involve solving a system of equations, a task that could be undertaken with mathematical software or through manual calculation.
-
Recursive Relationships: A recursive relationship involves defining a term based on preceding terms. This approach demands a careful consideration of various combinations and potential recursive functions.
Beyond the Obvious: Exploring Deeper Mathematical Concepts
The lack of an immediately apparent pattern invites us to consider more sophisticated mathematical techniques and concepts. Let's delve into some of these:
The Power of Mathematical Modeling
Mathematical modeling involves creating a mathematical representation of a real-world phenomenon or a set of data. In our case, the sequence 1 1 2 4 3 9 can be considered the data. We can try to find a model – a function or equation – that accurately describes this data. This could involve techniques like curve fitting, polynomial interpolation, or even more advanced statistical modeling methods. The key is finding a model that not only fits the known terms but also allows for the prediction of future terms in the sequence.
Statistical Analysis: Unveiling Hidden Correlations
If a simple mathematical pattern remains elusive, statistical analysis can help identify hidden relationships within the data. Techniques such as correlation analysis could reveal hidden correlations between the numbers or with other mathematical functions. This might uncover unexpected patterns or suggest alternative interpretations of the sequence. While statistical analysis might not provide a definitive "solution," it can offer valuable insights and inform further investigation.
The Importance of Context: The Sequence in a Broader Perspective
The interpretation of a mathematical sequence often depends on its context. Where did this sequence originate? Was it generated randomly? Is it part of a larger problem or puzzle? Without additional information, the possibilities remain open. The lack of clear context emphasizes the need for careful consideration and the exploration of various interpretations.
The sequence could be:
-
Part of a larger, more complex sequence: The provided sequence may be just a segment of a much larger and more intricate pattern. Discovering the full sequence could reveal the underlying rule governing its progression.
-
A result of a specific algorithm: A computer program or algorithm might generate the sequence based on a set of instructions. Understanding the algorithm could illuminate the pattern.
-
A coded message: The sequence could represent a coded message or a cipher, requiring decryption techniques to reveal its true meaning.
Enhancing Critical Thinking and Problem-Solving Skills
The sequence 1 1 2 4 3 9 serves as an excellent tool for honing critical thinking and problem-solving skills. The challenge lies not just in finding a single "correct" answer, but in exploring various approaches, analyzing potential patterns, and developing a deeper understanding of mathematical concepts. The process itself is as important as the outcome, fostering creativity, perseverance, and a willingness to explore multiple avenues of inquiry.
The Value of Perseverance and Exploration
The pursuit of deciphering this seemingly simple sequence underscores the importance of perseverance. The lack of an immediately apparent pattern can be frustrating. However, this challenge is exactly what makes the problem engaging. The ability to continue searching, even when faced with setbacks, is a valuable asset in any field.
Bridging the Gap Between Theory and Application
Mathematical problems, such as this numerical sequence, offer a tangible way to bridge the gap between theoretical knowledge and practical application. The process of solving the problem encourages engagement with mathematical concepts and techniques, solidifying understanding and fostering a deeper appreciation for the beauty and power of mathematics.
Conclusion: The Enduring Mystery and the Ongoing Quest
The sequence 1 1 2 4 3 9 presents a compelling puzzle, showcasing the beauty of mathematics and the power of human ingenuity. While a definitive, universally accepted solution might remain elusive, the very act of exploration is rewarding. The process encourages us to engage with various mathematical concepts, hone our critical thinking skills, and appreciate the inherent allure of pattern recognition and mathematical discovery. The journey of unraveling this sequence is a journey of mathematical exploration, offering a glimpse into the fascinating world of numbers and patterns. The mystery persists, inviting further investigation and highlighting the enduring appeal of mathematical challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 1 2 4 3 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.