1 1 3 Plus 1 1 3
News Co
May 08, 2025 · 5 min read
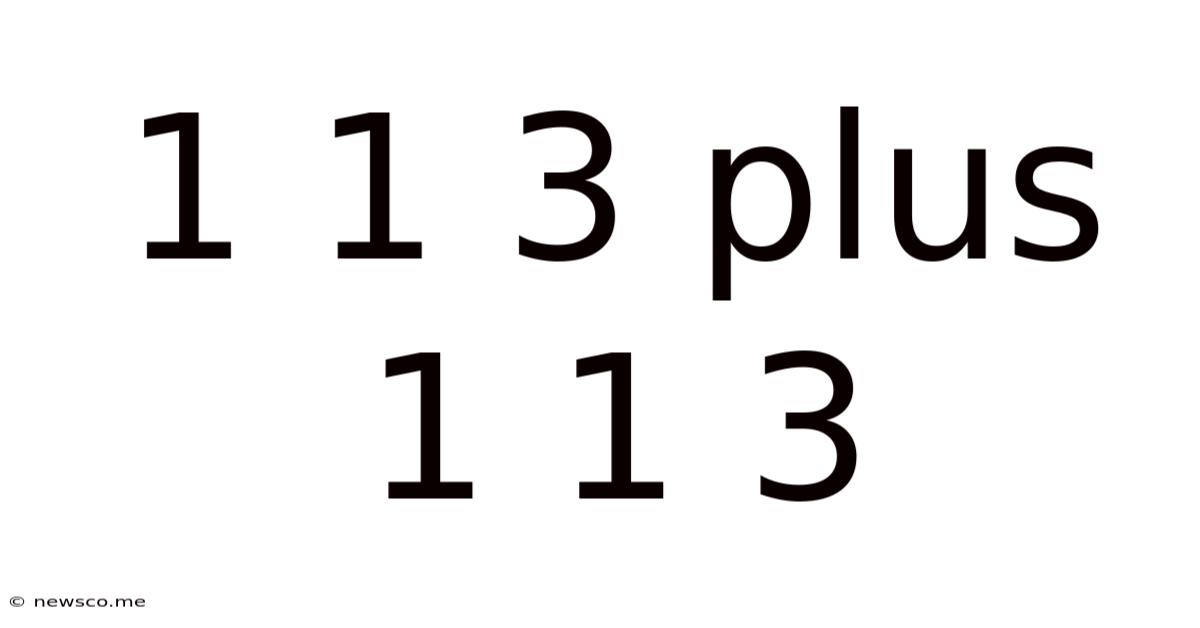
Table of Contents
1 1 3 Plus 1 1 3: Unpacking the Enigma of Simple Repetition
The seemingly simple numerical sequence "1 1 3 plus 1 1 3" might appear trivial at first glance. However, a deeper dive reveals a fascinating exploration into the realms of mathematics, pattern recognition, symbolic representation, and even the potential for creative interpretation. This article will dissect this sequence from various perspectives, revealing its hidden complexities and surprising implications.
Mathematical Interpretations
The most straightforward approach is to treat this as a basic arithmetic problem. "1 1 3 plus 1 1 3" could be interpreted in several ways depending on the intended grouping and operation:
Option 1: Concatenation and Addition
One possible interpretation is to treat the sequences "1 1 3" as single numerical entities. This would involve concatenating the digits to form the numbers 113. The problem then becomes: 113 + 113 = 226. This is a straightforward addition problem with a clear and concise answer.
Option 2: Separate Addition of Digits
Alternatively, we could interpret each digit separately and add them: (1 + 1 + 3) + (1 + 1 + 3) = 5 + 5 = 10. This approach emphasizes the individual components of the sequence and demonstrates a different mathematical outcome.
Option 3: Exploring Base Systems
The problem could also be analyzed through the lens of different base systems. While our standard system is base-10, exploring other bases (like binary or hexadecimal) could lead to unique interpretations. For instance, in base 2 (binary), "1 1 3" doesn't directly translate, as 3 is outside the binary system's two-digit range (0 and 1). However, analyzing this through a base conversion lens could open up more complex mathematical discussions.
Symbolic and Pattern Recognition
Moving beyond the purely numerical, let's explore the symbolic representation and pattern recognition inherent in the sequence "1 1 3 plus 1 1 3."
Repetition and Emphasis
The repetition of "1 1 3" creates a strong sense of emphasis and rhythm. This repetition immediately draws attention and suggests a potential underlying structure or meaning beyond simple arithmetic. In music, for example, the repetition of a melodic motif builds familiarity and anticipation. Similarly, the repeated "1 1 3" sequence in this context can be viewed as a symbolic unit with its own unique characteristics.
Potential for Sequence Continuation
The repetitive nature of the sequence naturally leads to the question: what comes next? Does the pattern continue (1 1 3 plus 1 1 3 plus 1 1 3…)? Could we create a recursive sequence based on this simple beginning? The answer depends entirely on how we choose to define the rules governing the sequence's continuation. This opens up possibilities for exploring mathematical concepts such as sequences, series, and their limits.
Connection to Fibonacci Sequence?
While not a direct representation, the appearance of the "1 1 3" sequence might evoke a subtle association with the Fibonacci sequence (1, 1, 2, 3, 5, 8...). The "3" appears in the Fibonacci sequence, and this tenuous connection could spark further investigation into mathematical relationships and sequences. However, it's crucial to note that this is a superficial association; there's no definitive mathematical link between "1 1 3 plus 1 1 3" and the Fibonacci sequence.
Creative and Interpretive Approaches
Beyond the purely mathematical realm, the sequence "1 1 3 plus 1 1 3" offers fertile ground for creative and interpretive exploration.
Artistic Interpretation
Visual artists might use this sequence as a starting point for creating works based on repetition, rhythm, and numerical symbolism. Imagine a piece of art where the numbers are represented by different colors, textures, or spatial arrangements, reflecting the repetitive structure of the sequence.
Musical Composition
A composer could create a piece of music using the sequence "1 1 3 plus 1 1 3" as a rhythmic or melodic motif. The repetition could be translated into musical phrases, creating a sense of structure and variation. Different instruments could represent the different numbers, or the numbers could be reflected in the musical dynamics (loudness and softness).
Literary Application
Writers could use the sequence as a symbolic element in a narrative, creating a sense of mystery or a recurring theme. The repetition could represent a cyclical event, a persistent problem, or a recurring character trait.
Expanding the Scope: Applications in Programming and Data Science
While seemingly simple, the concept of repeating numerical sequences and their manipulation has wide-ranging applications in computer programming and data science.
Array Manipulation
In programming, the sequence "1 1 3" could be easily represented as an array or list. Manipulating this array, such as repeating or modifying its elements, is a fundamental programming task.
Data Structures
Data structures, such as linked lists, stacks, or queues, are designed to handle sequential data. Understanding how to process a sequence like "1 1 3 plus 1 1 3" within these structures is vital for efficient data management.
Algorithm Design
Designing algorithms that process repeated patterns is a crucial element of many programming tasks, especially in domains like image processing, signal processing, and time series analysis. The principles underlying the analysis of "1 1 3 plus 1 1 3" are directly applicable to these algorithmic challenges.
Conclusion: The Unexpected Depth of Simplicity
The seemingly simple expression "1 1 3 plus 1 1 3" has, through this exploration, revealed a surprising level of complexity and potential for interpretation. From straightforward arithmetic calculations to sophisticated symbolic and artistic applications, this sequence challenges us to think beyond the immediate and to consider the hidden depths that often lie within the simplest of expressions. It serves as a potent reminder of the interconnectedness of seemingly disparate fields—mathematics, art, music, and computer science—and the limitless potential for creative exploration within seemingly mundane numerical sequences. The sequence’s simplicity is a deceptive mask for its multifaceted nature, offering a fertile ground for continued investigation and inspiration. This seemingly simple puzzle invites us to continuously explore its depths and discover its hidden meanings and potential.
Latest Posts
Latest Posts
-
An Angle That Measures Exactly 90 Degrees
May 08, 2025
-
How Much Is 6 Weeks In Days
May 08, 2025
-
3 To The Power Of 1 3
May 08, 2025
-
What Is The Reciprocal Of 8 9
May 08, 2025
-
What Is The Common Factor Of 20
May 08, 2025
Related Post
Thank you for visiting our website which covers about 1 1 3 Plus 1 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.