1 1 Sin X 1 1 Sin X
News Co
Apr 26, 2025 · 5 min read
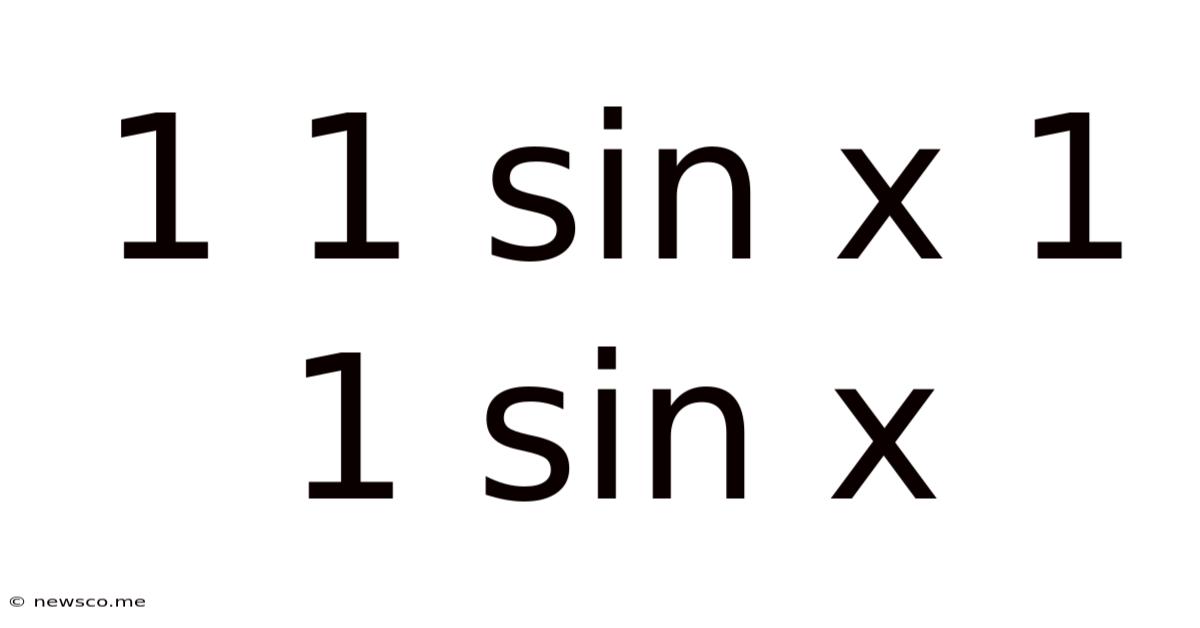
Table of Contents
- 1 1 Sin X 1 1 Sin X
- Table of Contents
- Decomposing the Expression: 1/(1 + sin x) - 1/(1 - sin x)
- Understanding the Expression
- Simplifying the Expression: A Step-by-Step Approach
- Verification and Domain Considerations
- Applications and Significance
- Expanding on Trigonometric Identities
- Problem-Solving Strategies in Trigonometry
- Conclusion
- Latest Posts
- Related Post
Decomposing the Expression: 1/(1 + sin x) - 1/(1 - sin x)
This article delves into the mathematical manipulation and simplification of the expression 1/(1 + sin x) - 1/(1 - sin x), exploring its trigonometric identities, potential applications, and its behavior across different domains. We'll examine the process of simplification, discuss the significance of the result, and explore how this type of problem-solving contributes to a deeper understanding of trigonometric functions.
Understanding the Expression
The given expression, 1/(1 + sin x) - 1/(1 - sin x), involves rational functions of trigonometric functions. Understanding its structure is crucial before attempting simplification. We have two fractions, each with a trigonometric expression in the denominator. The numerators are both 1, and the denominators are conjugate pairs: (1 + sin x) and (1 - sin x). This observation will play a crucial role in our simplification strategy.
Simplifying the Expression: A Step-by-Step Approach
To simplify this expression, we need to find a common denominator and then combine the fractions. The least common denominator (LCD) is the product of the two denominators: (1 + sin x)(1 - sin x).
-
Finding the Common Denominator:
We rewrite each fraction with the common denominator:
[1/(1 + sin x)] * [(1 - sin x)/(1 - sin x)] - [1/(1 - sin x)] * [(1 + sin x)/(1 + sin x)] -
Combining the Fractions:
Now that both fractions have the same denominator, we can combine them:
[(1 - sin x) - (1 + sin x)] / [(1 + sin x)(1 - sin x)] -
Simplifying the Numerator:
Expanding the numerator, we get:
(1 - sin x - 1 - sin x) / [(1 + sin x)(1 - sin x)]This simplifies to:
(-2sin x) / [(1 + sin x)(1 - sin x)] -
Simplifying the Denominator (Difference of Squares):
Notice that the denominator is a difference of squares: (a + b)(a - b) = a² - b². In this case, a = 1 and b = sin x. Therefore:
(1 + sin x)(1 - sin x) = 1² - (sin x)² = 1 - sin²x -
Using the Pythagorean Identity:
Recall the fundamental Pythagorean identity in trigonometry: sin²x + cos²x = 1. We can rearrange this to get: cos²x = 1 - sin²x. Substituting this into our expression, we have:
(-2sin x) / cos²x -
Final Simplified Form:
Our simplified expression is:
-2sin x / cos²xwhich can also be written as-2(sin x / cos x)(1/cos x) = -2tan x sec x
Verification and Domain Considerations
The simplified expression -2tan x sec x is equivalent to the original expression, 1/(1 + sin x) - 1/(1 - sin x), except for values of x where the original expression is undefined.
Points of Undefined Values:
The original expression is undefined when either (1 + sin x) = 0 or (1 - sin x) = 0. This occurs when sin x = 1 or sin x = -1. Therefore, the expression is undefined at x = π/2 + nπ, where n is any integer. Our simplified expression, -2tan x sec x, shares the same undefined points because tan x and sec x are undefined at these values.
This highlights the importance of checking for the domain of validity when simplifying trigonometric expressions.
Applications and Significance
This type of simplification is frequently encountered in calculus, particularly when dealing with integrals and derivatives involving trigonometric functions. The simplified form, -2tan x sec x, is often easier to work with in these contexts. For example, if you were to integrate the original expression, the simplified form would greatly reduce the complexity of the integration process.
Furthermore, understanding how to manipulate trigonometric expressions is fundamental to solving various problems in physics, engineering, and other fields where trigonometric functions are used to model oscillatory or periodic phenomena.
Expanding on Trigonometric Identities
The simplification process heavily relied on the Pythagorean identity (sin²x + cos²x = 1). Let's briefly explore other relevant trigonometric identities that might be useful in similar simplification problems:
-
Reciprocal Identities: These relate the basic trigonometric functions (sin x, cos x, tan x) to their reciprocals (csc x, sec x, cot x). For example: sec x = 1/cos x, csc x = 1/sin x, cot x = 1/tan x.
-
Quotient Identities: These establish the relationships between tangent and cotangent to sine and cosine. For example: tan x = sin x / cos x, cot x = cos x / sin x.
-
Angle Sum and Difference Identities: These identities help simplify expressions involving the sum or difference of angles. For example: sin(x + y) = sin x cos y + cos x sin y, cos(x - y) = cos x cos y + sin x sin y.
-
Double and Half-Angle Identities: These are used to simplify expressions involving double or half angles. For example: sin 2x = 2sin x cos x, cos 2x = cos²x - sin²x = 1 - 2sin²x = 2cos²x - 1.
Problem-Solving Strategies in Trigonometry
When faced with complex trigonometric expressions, a systematic approach is crucial. Here's a suggested strategy:
-
Identify the Key Trigonometric Functions: Determine the main trigonometric functions present in the expression (sin, cos, tan, etc.).
-
Look for Familiar Identities: Try to recognize any trigonometric identities that might be applicable. This often involves searching for patterns like differences of squares, Pythagorean identities, or sum-to-product formulas.
-
Simplify Step-by-Step: Break down the simplification process into manageable steps. This helps avoid errors and makes it easier to track progress.
-
Verify Your Result: After simplifying, check your work by substituting specific values for x (avoiding points of discontinuity) into both the original and simplified expressions. If the results match, it's a strong indication that your simplification is correct.
-
Consider the Domain: Always be mindful of the domain of the original expression and ensure that your simplification doesn't introduce any additional restrictions.
Conclusion
The simplification of 1/(1 + sin x) - 1/(1 - sin x) to -2tan x sec x demonstrates the power of trigonometric identities and algebraic manipulation. This process highlights the interconnectedness of trigonometric functions and the importance of a systematic approach to solving trigonometric problems. A thorough understanding of these concepts is invaluable in various fields, including mathematics, physics, and engineering. By mastering these techniques, you equip yourself with the tools to tackle more complex trigonometric challenges efficiently and accurately. Remember to always check your domain restrictions to ensure the validity of your simplified expressions across all relevant values of x.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 1 Sin X 1 1 Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.