1/2 Divided By 2/3 As A Fraction
News Co
May 08, 2025 · 5 min read
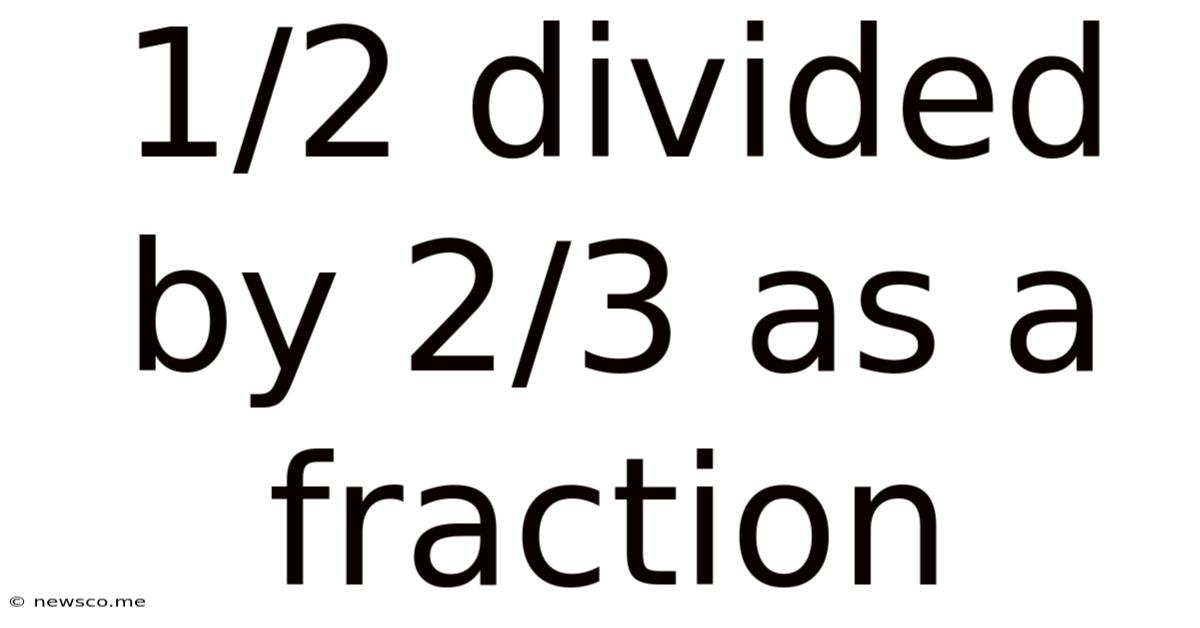
Table of Contents
1/2 Divided by 2/3 as a Fraction: A Comprehensive Guide
Understanding fractions and how to manipulate them is a fundamental skill in mathematics. While seemingly simple, operations involving fractions can sometimes feel confusing. This comprehensive guide will delve into the process of dividing fractions, specifically focusing on the problem of 1/2 divided by 2/3. We'll not only solve the problem but also explore the underlying principles, providing you with a solid grasp of the concept and the ability to tackle similar problems with confidence.
Understanding Fraction Division
Before diving into the specific calculation, let's establish a solid understanding of fraction division. Dividing fractions differs significantly from adding, subtracting, or even multiplying them. The core principle lies in understanding the concept of reciprocals.
What is a Reciprocal?
A reciprocal, also known as the multiplicative inverse, is a number that, when multiplied by the original number, results in 1. To find the reciprocal of a fraction, simply swap the numerator and the denominator. For example:
- The reciprocal of 2/3 is 3/2.
- The reciprocal of 5/7 is 7/5.
- The reciprocal of 1 is 1 (since 1 x 1 = 1).
The Rule of Fraction Division
The golden rule of fraction division is: To divide by a fraction, multiply by its reciprocal. This seemingly simple rule is the key to unlocking the seemingly complex world of fraction division.
Solving 1/2 Divided by 2/3
Now, let's apply this rule to our specific problem: 1/2 divided by 2/3.
Following the rule, we replace the division operation with multiplication and use the reciprocal of the second fraction:
1/2 ÷ 2/3 = 1/2 * 3/2
Now, we multiply the numerators together and the denominators together:
(1 * 3) / (2 * 2) = 3/4
Therefore, 1/2 divided by 2/3 equals 3/4.
Visualizing Fraction Division
While the mathematical process is straightforward, visualizing the division can enhance understanding. Imagine you have half a pizza (1/2). You want to divide this half pizza into portions that are each 2/3 the size of a whole pizza. How many of these 2/3 portions can you get from your half pizza? The answer, as we've calculated, is 3/4 of a portion. It's less than one full portion because the portions you're dividing by are larger than the amount of pizza you have.
Expanding on Fraction Division Concepts
Let's expand on the concepts to further solidify your understanding and tackle more complex scenarios.
Dividing Fractions with Whole Numbers
When dividing a fraction by a whole number, remember that a whole number can be expressed as a fraction with a denominator of 1. For example:
2/5 ÷ 2 = 2/5 ÷ 2/1 = 2/5 * 1/2 = 2/10 = 1/5
Dividing Fractions with Mixed Numbers
Mixed numbers, which combine whole numbers and fractions (like 1 1/2), require an extra step before applying the division rule. You must first convert the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to the denominator.
For instance, let's solve 1 1/2 divided by 2/3:
-
Convert the mixed number to an improper fraction: 1 1/2 = (1 * 2 + 1) / 2 = 3/2
-
Apply the division rule: 3/2 ÷ 2/3 = 3/2 * 3/2 = 9/4
-
Simplify if necessary: 9/4 can be expressed as the mixed number 2 1/4.
Simplifying Fractions
After performing the multiplication in fraction division, always simplify the resulting fraction if possible. Simplification means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
For example, in the problem 6/10, the GCD of 6 and 10 is 2. Dividing both by 2 gives us the simplified fraction 3/5.
Real-World Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems; it has numerous practical applications in everyday life and various professions.
- Cooking: Dividing recipes, adjusting ingredient quantities based on the number of servings.
- Sewing: Calculating fabric requirements, dividing patterns.
- Construction: Measuring and dividing materials for building projects.
- Engineering: Calculating ratios and proportions in designing structures and systems.
- Finance: Dividing shares, calculating percentages and proportions of investments.
Troubleshooting Common Mistakes in Fraction Division
Even with a clear understanding of the rules, certain common mistakes can occur when working with fraction division. Let's address these potential pitfalls:
- Forgetting to use the reciprocal: This is the most frequent error. Always remember to multiply by the reciprocal of the second fraction, not the first.
- Incorrectly multiplying numerators and denominators: Double-check your calculations to ensure accurate multiplication of both the numerators and the denominators.
- Failing to simplify the answer: Always reduce your final answer to its simplest form.
Practicing Fraction Division
The best way to master fraction division is through consistent practice. Try solving various problems with increasing complexity, starting with simple fractions and gradually progressing to more challenging ones involving mixed numbers and larger values. Online resources and workbooks offer a wide range of practice problems to hone your skills.
Conclusion: Mastering Fraction Division
Fraction division, while initially appearing complex, becomes manageable with a thorough understanding of the principles involved. By consistently applying the rule of multiplying by the reciprocal and practicing regularly, you'll build confidence and proficiency in this essential mathematical skill. Remember to visualize the problem, check for simplification opportunities, and always double-check your calculations to avoid common mistakes. Mastering fraction division opens doors to a deeper understanding of mathematics and its widespread applications in various fields. So, continue practicing, and you'll find that conquering fractions is an achievable and rewarding journey.
Latest Posts
Latest Posts
-
Examples Of Line Segments In Real Life
May 08, 2025
-
What Is 15 8 As A Decimal
May 08, 2025
-
How Many Months With 5 Weeks
May 08, 2025
-
The Symbol For Population Variance Is
May 08, 2025
-
How To Find X In Y Mx B
May 08, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 2/3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.