1 2x 1 2x X 1
News Co
Apr 16, 2025 · 5 min read
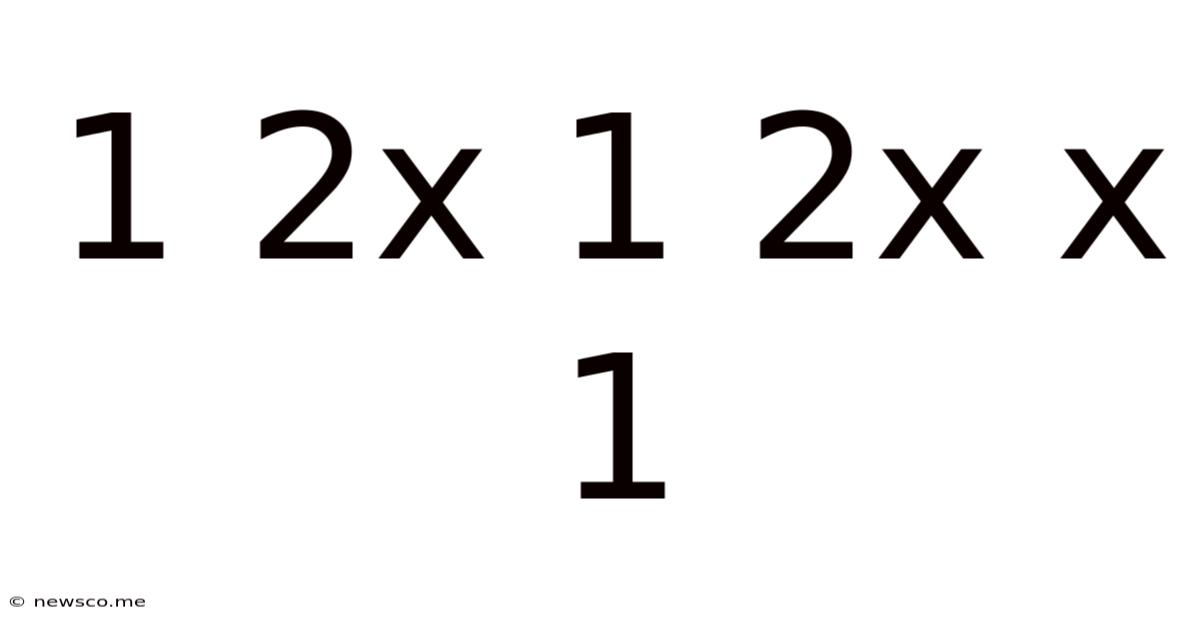
Table of Contents
Decoding the Mystery: A Deep Dive into 1 2x 1 2x x 1
The seemingly simple sequence "1 2x 1 2x x 1" might appear innocuous at first glance. However, this short string of numbers and symbols hides a surprising depth of potential interpretations, depending on the context and the rules we apply. This article delves into the various possibilities, exploring mathematical perspectives, pattern recognition, coding implications, and even venturing into the realm of potential symbolic meaning. Our exploration will highlight the importance of context in interpreting seemingly simple sequences and showcase the power of analytical thinking in uncovering hidden structures.
Mathematical Interpretations: Beyond the Obvious
The most straightforward interpretation treats "x" as a variable. This allows us to approach the sequence from several mathematical angles:
1. As an Algebraic Expression
If we view the sequence as a rudimentary algebraic expression, we can try to find relationships between the numbers and the variable 'x'. One possibility is to assume a pattern based on multiplication or addition. For instance, it might represent a fragmented equation, leaving the solution to 'x' undefined without additional information. To illustrate:
-
Scenario 1 (Multiplication): We could hypothesize a pattern where each number is multiplied by a successive value. This approach, however, fails to produce a coherent mathematical relationship based on the given sequence.
-
Scenario 2 (Addition/Subtraction): This approach might suggest exploring patterns using addition or subtraction, seeking a consistent operation between adjacent terms. Again, without additional context, we lack sufficient data to determine a consistent mathematical rule.
-
Scenario 3 (Polynomial Representation): More complex mathematical interpretations might involve representing the sequence as a polynomial. A polynomial could be constructed such that the provided values (1, 2x, 1, 2x, x, 1) form a set of points on the polynomial’s graph. However, this requires further assumptions about the degree of the polynomial and its underlying structure. This necessitates having more data points to define the polynomial accurately.
2. Exploring Potential Equations
Without a defined operation connecting the elements, we can't solve for 'x'. We need more context or additional information. This could be:
- An accompanying equation: Another mathematical expression which clarifies the relationship between the numbers and 'x'.
- Boundary conditions: Constraints or limits which define the possible values of 'x'.
- A specific problem statement: Defining the goal or objective that the sequence is aiming to achieve.
Pattern Recognition and Sequences
Stepping away from pure algebraic manipulation, let's consider pattern recognition. The sequence itself exhibits a degree of symmetry: 1, 2x, 1, 2x. The 'x' breaks the perfect mirror symmetry, and the ending '1' adds another layer of complexity. This suggests:
1. Incomplete or Fragmented Pattern
The sequence might be a fragment of a larger, more elaborate pattern. Additional terms would be necessary to identify the overall governing rule. This requires more information to deduce the nature of the pattern.
2. Contextual Clues are Crucial
The sequence's meaning heavily relies on the context in which it is presented. Imagine it appearing within:
- A programming context: The sequence could represent elements in an array or parts of a code snippet.
- A cryptographic context: It could be a part of a cipher, where 'x' represents an unknown key or value.
- A mathematical puzzle: The puzzle itself might contain clues or constraints that reveal the underlying logic.
Coding Implications: Data Structures and Algorithms
Let's analyze the sequence from a computational perspective.
1. Data Structure Representation
The sequence can be represented in various programming data structures, such as:
- Arrays: A simple one-dimensional array could efficiently store the sequence.
- Lists: A linked list could be used, although it's less efficient for this particular sequence's simple access patterns.
- Sets: A set would be inappropriate as sets by definition must not contain duplicate values, which are present.
2. Algorithmic Processing
The nature of algorithms used to process the sequence depend on the desired outcome. For example, if the sequence is a part of a larger dataset, algorithms for pattern recognition, machine learning, or data mining could be employed.
3. Symbolic Representation
In many programming languages, 'x' would be treated as a variable. The interpretation would vary based on the programming language and the way the variable 'x' is defined and used within the code.
Symbolic and Abstract Interpretations
Moving beyond mathematical and computational realms, we can explore the possibility of the sequence representing a symbolic message.
1. Coded Messages and Cryptography
The inclusion of 'x' might suggest the sequence could form part of a cipher, similar to how the unknown values within a substitution cipher necessitate a key to decrypt a message.
2. Abstract Representation
Without concrete context, the sequence can be seen as an abstract representation of a more complex underlying concept. It might symbolize a transition, a fluctuation, or a progression. The inclusion of 'x' adds an element of uncertainty or an unknown variable affecting this transition.
The Power of Context and Further Exploration
The seemingly simple "1 2x 1 2x x 1" sequence reveals the crucial role of context in interpretation. Without additional information, we can only speculate about its meaning. However, by considering it from various perspectives – mathematical, computational, and symbolic – we've illustrated the richness of potential meanings hidden within seemingly simple sequences.
To fully understand this sequence, we need answers to critical questions:
- What is the source of this sequence? The origin (a textbook problem, a code snippet, a puzzle) significantly impacts interpretation.
- What is the intended outcome? Is it meant to be solved, decoded, analyzed, or is it just part of a larger process?
- Are there accompanying instructions or constraints? Additional information is crucial to disambiguate the sequence.
The exploration presented here only scratches the surface. Future investigation might explore:
- More sophisticated mathematical models: Investigating more complex mathematical structures that could potentially incorporate this sequence.
- Advanced pattern recognition techniques: Employing machine learning algorithms to uncover hidden patterns within extended versions of this sequence (if available).
- Cryptographic analysis: If a coded message is suspected, techniques from cryptography would be invaluable.
Ultimately, "1 2x 1 2x x 1" serves as a reminder of the importance of considering multiple perspectives and the necessity of context in interpreting data and information. Its ambiguity encourages analytical thinking and problem-solving skills. The true meaning lies not within the sequence itself, but within the context which provides the necessary framework for its understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 2x 1 2x X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.