1 3 1 3 1 3 1 3
News Co
May 07, 2025 · 6 min read
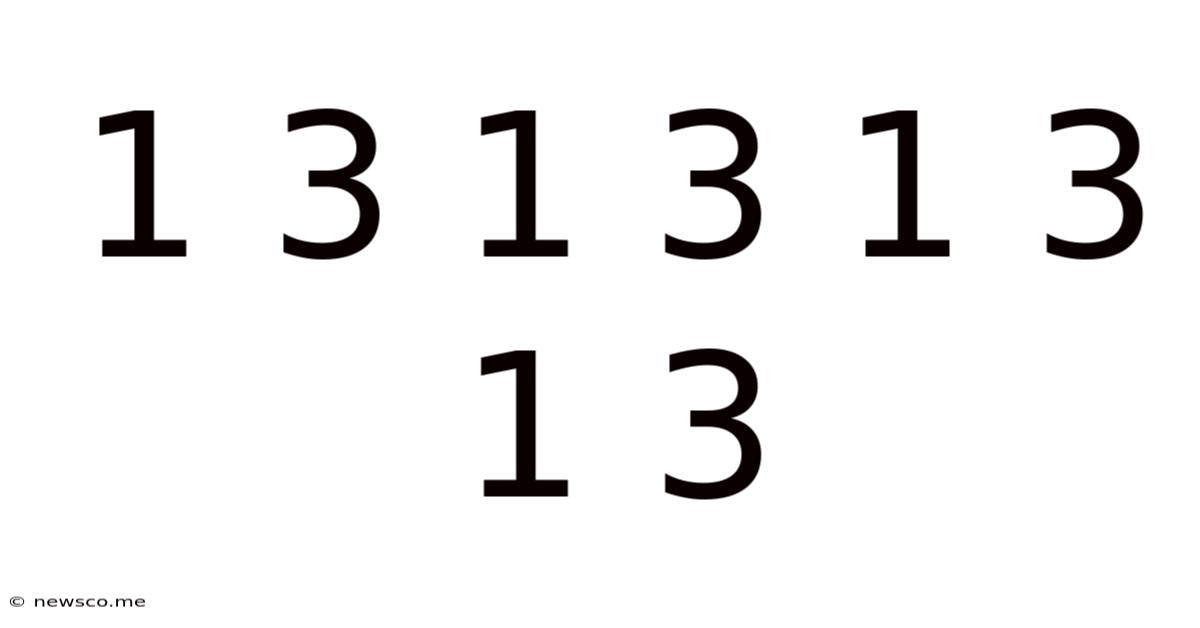
Table of Contents
Decoding the Rhythm: Exploring the Musical and Mathematical Significance of 1 3 1 3 1 3 1 3
The seemingly simple numerical sequence "1 3 1 3 1 3 1 3" might appear unremarkable at first glance. However, this rhythmic pattern holds a surprisingly rich significance across diverse fields, from musical composition to mathematical analysis and even the natural world. This article delves into the multifaceted interpretations and applications of this sequence, exploring its underlying structure, its prevalence in various creative endeavors, and its potential for further exploration.
The Musical Resonance of 1 3 1 3 1 3 1 3
In music, the sequence "1 3 1 3 1 3 1 3" can represent a rhythmic motif, a foundational element that shapes a piece's overall feel and structure. Interpreting the numbers as durations, with '1' representing a short note and '3' representing a longer note (e.g., a quarter note and a dotted quarter note, respectively), we find a rhythmic pattern that's both engaging and easily memorable.
Building Rhythmic Complexity
This simple sequence serves as a perfect building block for more complex rhythmic structures. By varying the note values associated with '1' and '3,' composers can create a wide range of rhythmic variations. For instance, '1' could be a sixteenth note and '3' an eighth note triplet, leading to a faster, more intricate feel. Conversely, '1' could represent a half note and '3' a dotted half note, resulting in a slower, more deliberate rhythm.
The flexibility of the 1 3 1 3 1 3 1 3 pattern allows for diverse musical expressions, from the playful and lighthearted to the solemn and profound. Its inherent asymmetry creates a sense of movement and anticipation, preventing monotony and keeping the listener engaged.
Syncopation and Emphasis
The alternation of short and long notes inherent in the sequence naturally lends itself to syncopation. Syncopation, the deliberate placement of accents on unexpected beats, adds a dynamic element to the music, creating a sense of rhythmic surprise and excitement. By strategically placing rests or emphasizing specific notes within the 1 3 1 3 1 3 1 3 framework, composers can further manipulate the rhythmic texture and create a unique musical voice.
Cross-Cultural Applications
While the specific interpretation of the sequence may vary across musical cultures, the underlying principle of contrasting rhythmic durations remains universal. The 1 3 1 3 1 3 1 3 pattern, or variations thereof, could easily find its place in diverse musical genres, from classical to jazz, pop to folk, demonstrating its inherent adaptability and cross-cultural applicability.
Mathematical Explorations: Patterns and Sequences
Beyond its musical applications, the 1 3 1 3 1 3 1 3 sequence holds mathematical intrigue. It can be viewed as a simple repeating sequence, a type of pattern readily analyzed using various mathematical tools.
Repeating Sequences and Periodicity
The sequence’s repetitive nature is a key feature, illustrating the concept of periodicity. Understanding periodicity is crucial in various mathematical fields, including signal processing, cryptography, and the study of dynamical systems. The sequence's regular pattern allows for easy prediction of subsequent terms, showcasing a fundamental concept of mathematical predictability.
Variations and Extensions
While the given sequence is straightforward, exploring its variations opens up avenues for mathematical investigation. What happens if we alter the ratio between the '1' and '3'? What if we introduce additional numbers into the sequence, creating a more complex, non-repeating pattern? These are questions that lead to exploring more advanced concepts within mathematics, like Fibonacci sequences or fractal patterns.
Relationship to Other Mathematical Concepts
The 1 3 1 3 1 3 1 3 sequence can be viewed as a simplified representation of more complex mathematical concepts. For example, it relates to the idea of rhythmic ratios in music theory, which itself has deep connections to mathematical proportions and harmonies. Further explorations could reveal relationships to other mathematical sequences or patterns, enriching our understanding of both the sequence and related mathematical concepts.
Beyond Music and Math: Applications in Other Fields
The 1 3 1 3 1 3 1 3 sequence, while seemingly simple, transcends the boundaries of music and mathematics. Its underlying principle of rhythmic variation and repetition finds surprising applications in other seemingly unrelated fields.
Nature's Rhythms: Biological and Ecological Patterns
Consider the rhythmic patterns observed in nature. The ebb and flow of tides, the cyclical patterns of predator-prey populations, or even the rhythmic beating of a heart – all demonstrate the prevalence of repetitive, yet variable, patterns. The 1 3 1 3 1 3 1 3 sequence, with its simple yet dynamic structure, serves as a rudimentary model for understanding these complex natural rhythms. It's a basic building block that can help us better understand the underlying mathematical principles governing many natural phenomena.
The Art of Movement: Dance and Choreography
In dance and choreography, the 1 3 1 3 1 3 1 3 sequence could represent a basic rhythmic framework for a movement sequence. The short and long durations could represent different movement types or intensities. This basic rhythmic structure could be combined with other movements to generate a sophisticated and dynamic dance piece, suggesting the universality of such patterns across various artistic mediums.
The Design World: Visual Rhythms and Patterns
Even in the visual arts, the concept of rhythm and pattern plays a crucial role. Think of the repeating motifs in architectural designs, the rhythmic arrangement of elements in painting and graphic design. The 1 3 1 3 1 3 1 3 sequence, though not directly visual, encapsulates the underlying principle of rhythmic variation and repetition that informs much of visual design.
Conclusion: A Simple Sequence with Profound Implications
The seemingly insignificant numerical sequence "1 3 1 3 1 3 1 3" reveals itself to be a surprisingly rich and versatile concept. Its applications span diverse fields, from the creative realms of music and dance to the analytical world of mathematics and the natural world. Its inherent simplicity belies its potential for complexity, providing a foundation for exploring more intricate rhythmic patterns, mathematical sequences, and even the natural world's underlying organization. The continued exploration of this sequence and its variations promises further insights into the interconnectedness of different disciplines and the beauty of underlying patterns that shape our world. Further research, particularly in the computational analysis of variations and the exploration of its applications in artificial intelligence and algorithmic composition, holds immense potential. The 1 3 1 3 1 3 1 3 sequence, despite its simplicity, is a testament to the power of basic patterns to create complexity and beauty across various domains. Its adaptability and versatility make it a compelling subject for continued investigation and creative exploration.
Latest Posts
Latest Posts
-
How Many Lines Of Symmetry Does The Polygon Have
May 08, 2025
-
Name A Pair Of Complementary Angles
May 08, 2025
-
What Is The Measure Of C In The Parallelogram Shown
May 08, 2025
-
1 625 Rounded To The Nearest Hundredth
May 08, 2025
-
1 Gallon Is Equal To How Many Ml
May 08, 2025
Related Post
Thank you for visiting our website which covers about 1 3 1 3 1 3 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.