1 3 4 2 1 2
News Co
May 08, 2025 · 5 min read
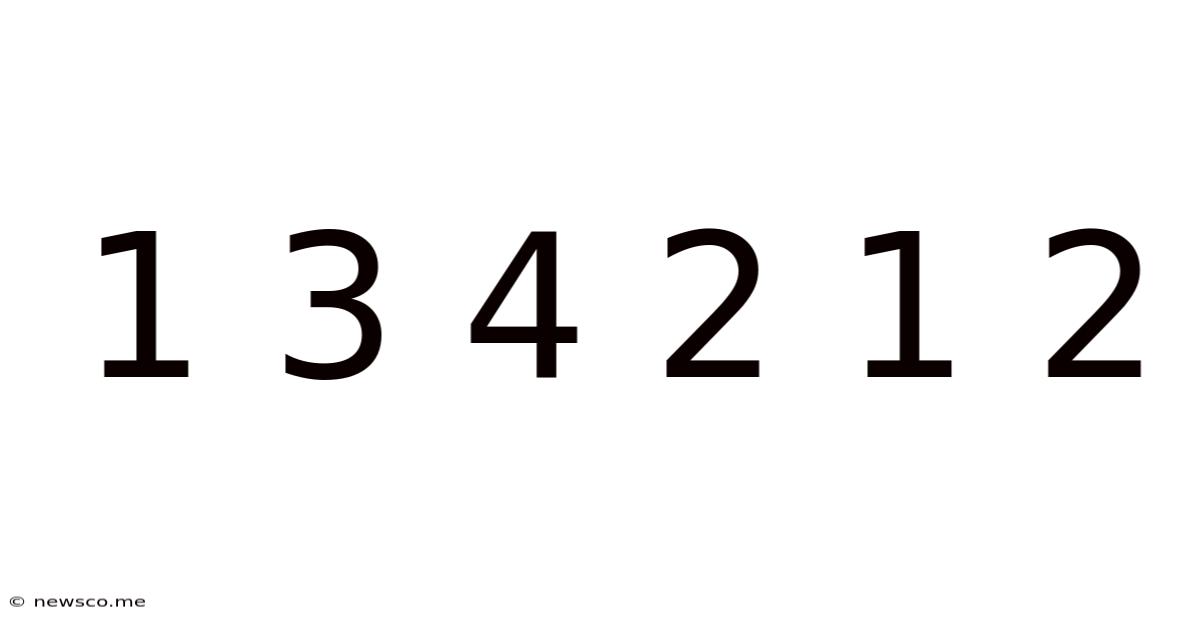
Table of Contents
Decoding the Sequence: 1 3 4 2 1 2 – A Deep Dive into Patterns, Possibilities, and Applications
The seemingly simple sequence "1 3 4 2 1 2" might appear innocuous at first glance. However, this numerical arrangement opens a door to a fascinating exploration of patterns, potential mathematical relationships, and diverse applications across various fields. This article will delve into the intricacies of this sequence, examining its potential interpretations, exploring its possible origins, and speculating on its practical uses. We'll use a multi-faceted approach, touching upon mathematical analysis, pattern recognition, and the broader context of sequence analysis in data science and beyond.
Is it Random? Assessing the Probability of Randomness
Before we embark on analyzing possible patterns, it's crucial to address the question of randomness. Is the sequence "1 3 4 2 1 2" truly random, or does it conceal an underlying structure? Purely random sequences, generated by processes like coin flips or dice rolls, follow specific statistical distributions. For instance, the probability of each number appearing in a truly random sequence should be approximately equal. In our case, the numbers 1 and 2 appear twice, while 3 and 4 appear only once. This slight discrepancy doesn't definitively prove non-randomness, as small deviations are expected even in random sequences of this length. However, it suggests the possibility of an underlying pattern.
Statistical Tests for Randomness
To further investigate, we could employ various statistical tests designed to detect deviations from randomness. These tests often analyze factors such as the frequency distribution of numbers, the autocorrelation between consecutive numbers, and the runs of consecutive identical numbers. Such tests would provide a quantitative measure of how likely it is that the sequence originated from a purely random process. While conducting these tests is beyond the scope of this article, it’s important to recognize the importance of rigorous statistical analysis in determining the nature of a sequence.
Searching for Patterns: Mathematical and Logical Interpretations
The absence of a clear, immediately obvious pattern doesn't preclude the existence of a deeper, more subtle structure. Let's explore some potential avenues for interpretation:
1. Permutation and Variation
The sequence might represent a specific permutation or variation of a larger set of numbers. For instance, if we consider the set {1, 2, 3, 4}, the sequence "1 3 4 2 1 2" could be a subset or a specific arrangement within a larger sequence involving this set. Analyzing the sequence's potential relationships to permutations and combinations could reveal underlying mathematical relationships.
2. Recursive or Iterative Patterns
Mathematical sequences often follow recursive or iterative rules. A recursive rule defines each term based on previous terms. An iterative rule involves applying a consistent operation to generate subsequent terms. For our sequence, we could try different recursive or iterative rules to see if they generate "1 3 4 2 1 2" or a similar sequence. This process might involve exploring various mathematical functions and operations.
3. Modular Arithmetic and Cyclical Patterns
Modular arithmetic deals with remainders after division. It's possible that the sequence exhibits cyclical behavior within a specific modulus. We could analyze the sequence's behavior modulo 2, 3, 4, or other integers to identify potential cyclical patterns. Such analysis might reveal a hidden structure based on modular arithmetic.
4. Relationship to Other Mathematical Sequences
The sequence could be a fragment or a variation of known mathematical sequences like Fibonacci sequences, Lucas numbers, or other recursively defined sequences. Exploring these connections could provide valuable insights into the sequence's origins and potential properties.
Beyond the Numbers: Applications in Different Fields
Even without a definitive mathematical interpretation, the sequence "1 3 4 2 1 2" could hold significance within different domains:
1. Cryptography and Codes
Short numerical sequences, even seemingly random ones, can find applications in cryptography and coding. They could be elements within a larger key, a component of a cipher, or part of a more complex code system. The sequence's apparent lack of obvious patterns might even enhance its security value.
2. Data Science and Pattern Recognition
In data science, identifying and interpreting patterns in numerical sequences is a fundamental task. The sequence "1 3 4 2 1 2" could serve as a simple example dataset for testing algorithms designed for pattern recognition and anomaly detection.
3. Music and Rhythmic Structures
Numerical sequences can be used to represent rhythmic patterns in music. The sequence "1 3 4 2 1 2" could represent the durations of notes in a musical phrase. Exploring this interpretation could lead to the creation of unique musical pieces based on the sequence.
4. Game Design and Artificial Intelligence
In game development, such sequences could be used to generate random events, control the behavior of non-player characters, or define patterns in game mechanics. In artificial intelligence, the sequence might serve as a small test case for algorithms involved in machine learning and sequence prediction.
Expanding the Analysis: Longer Sequences and Data Sets
To deepen our understanding, we need to consider the possibility that "1 3 4 2 1 2" is merely a segment of a much longer sequence. If more data were available, we could apply more sophisticated statistical techniques and pattern recognition algorithms. The additional data points could unveil a hidden structure not apparent in the initial short sequence.
The Importance of Context
Understanding the context in which the sequence was obtained is crucial. If the sequence arose from a specific experiment, observation, or process, the underlying context might provide essential clues about its meaning and interpretation. Without knowing the source or the method of generation, our analysis remains somewhat limited.
Conclusion: The Ongoing Quest for Meaning
The sequence "1 3 4 2 1 2" serves as a microcosm of the broader challenge of interpreting patterns and extracting meaning from numerical data. While we haven't arrived at a definitive explanation for this particular sequence, our exploration highlights the various analytical techniques and potential applications that such sequences can possess. The ongoing pursuit of pattern recognition and meaning-making within numerical sequences remains a vital aspect of numerous scientific and technological fields. Further investigation, particularly with more data or additional context, would be necessary to reach a more conclusive understanding. The seemingly simple sequence "1 3 4 2 1 2" thus underscores the rich potential hidden within seemingly simple numerical patterns.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 3 4 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.