1/4 Divided By 4 As A Fraction
News Co
May 03, 2025 · 5 min read
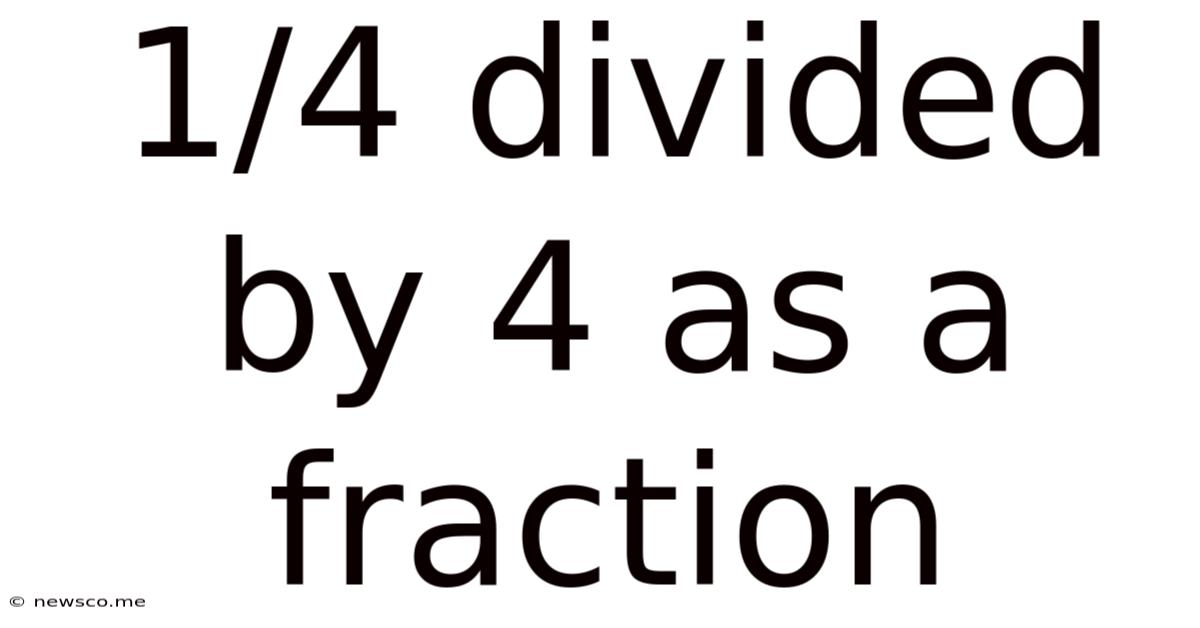
Table of Contents
1/4 Divided by 4: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with widespread applications. This comprehensive guide will walk you through the process of dividing the fraction 1/4 by 4, explaining the underlying principles and providing various approaches to solve this problem and similar ones. We'll delve into the mechanics, provide real-world examples, and explore different methods to solidify your understanding.
Understanding Fraction Division
Before tackling 1/4 divided by 4, let's review the basics of fraction division. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Key Concept: Dividing by a whole number is equivalent to dividing by that whole number written as a fraction (with a denominator of 1). Thus, dividing 1/4 by 4 is the same as dividing 1/4 by 4/1.
Method 1: Using Reciprocals
This is the most common and generally preferred method. To divide fractions, we follow these steps:
-
Find the reciprocal: The reciprocal of 4 (or 4/1) is 1/4.
-
Change division to multiplication: Replace the division sign (÷) with a multiplication sign (×).
-
Multiply the fractions: Multiply the numerator (top number) of the first fraction by the numerator of the second fraction, and the denominator (bottom number) of the first fraction by the denominator of the second fraction.
Let's apply this to 1/4 divided by 4:
1/4 ÷ 4 = 1/4 × 1/4 = (1 × 1) / (4 × 4) = 1/16
Therefore, 1/4 divided by 4 equals 1/16.
Method 2: Visual Representation
Visualizing the problem can make it easier to grasp. Imagine you have a pizza cut into four equal slices (representing 1/4 of a whole pizza). Now, you want to divide this 1/4 slice into four equal parts. How big would each of those smaller pieces be?
To represent this visually, imagine dividing each of the four original pizza slices into four equal parts. You'd now have a total of 16 slices. Your original 1/4 slice would now be represented by 4 of these smaller slices. Dividing that 1/4 slice into four equal parts means each smaller piece represents 1/16 of the whole pizza. Therefore, 1/4 divided by 4 equals 1/16.
Method 3: Converting to Decimal
While not always the most efficient method for fraction problems, converting to decimals can help visualize the process:
-
Convert the fraction to a decimal: 1/4 is equal to 0.25.
-
Perform the division: Divide 0.25 by 4: 0.25 ÷ 4 = 0.0625
-
Convert back to a fraction (if needed): 0.0625 can be expressed as 625/10000. Simplifying this fraction by dividing both numerator and denominator by 625 gives us 1/16.
This method reaffirms that 1/4 divided by 4 equals 1/16.
Real-World Applications
Understanding fraction division is crucial in various real-world scenarios:
-
Cooking and Baking: Dividing recipes or ingredients. If a recipe calls for 1/4 cup of sugar and you want to make only a quarter of the recipe, you would need to divide 1/4 cup by 4, resulting in 1/16 cup of sugar.
-
Sewing and Crafting: Calculating fabric or material requirements. Dividing fabric pieces to create smaller components.
-
Sharing Resources: Dividing resources equally among a group of people. For instance, if you have 1/4 of a pie and want to share it equally amongst four friends, each friend would receive 1/16 of the pie.
-
Construction and Engineering: Precise measurements and calculations for projects, often involving fractions.
-
Financial Calculations: Dividing investments or calculating portions of budgets.
Solving Similar Problems: A Step-by-Step Guide
Let's extend our understanding by solving a few similar problems using the reciprocal method:
Problem 1: 2/3 divided by 5
-
Write as a fraction: 2/3 ÷ 5/1
-
Find the reciprocal: The reciprocal of 5/1 is 1/5.
-
Multiply: 2/3 × 1/5 = (2 × 1) / (3 × 5) = 2/15
Therefore, 2/3 divided by 5 equals 2/15.
Problem 2: 3/8 divided by 2/5
-
Find the reciprocal: The reciprocal of 2/5 is 5/2.
-
Multiply: 3/8 × 5/2 = (3 × 5) / (8 × 2) = 15/16
Therefore, 3/8 divided by 2/5 equals 15/16.
Problem 3: 5/6 divided by 1/3
-
Find the reciprocal: The reciprocal of 1/3 is 3/1.
-
Multiply: 5/6 × 3/1 = (5 × 3) / (6 × 1) = 15/6
-
Simplify: 15/6 can be simplified by dividing both numerator and denominator by 3, resulting in 5/2 or 2 1/2.
Therefore, 5/6 divided by 1/3 equals 5/2 or 2 1/2.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, here are some areas to explore:
-
Complex Fractions: These involve fractions within fractions. Mastering fraction division is essential for simplifying complex fractions.
-
Mixed Numbers: Learning to convert mixed numbers (e.g., 2 1/2) into improper fractions before performing division is crucial.
-
Algebraic Expressions: Applying fraction division to solve equations and inequalities containing fractions.
-
Applications in Calculus: Fraction division plays a role in various calculus concepts, including derivatives and integrals.
Conclusion: Mastering Fraction Division
Mastering fraction division is a cornerstone of mathematical proficiency. By understanding the principles of reciprocals, visualizing the problem, and practicing with various examples, you can confidently tackle fraction division problems of increasing complexity. Remember the core concept: dividing by a fraction is the same as multiplying by its reciprocal. With consistent practice and a clear understanding of the underlying concepts, you'll build a strong foundation in fractions and their applications in various aspects of life. Remember to always simplify your answers to their lowest terms for the most accurate and efficient representation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1/4 Divided By 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.