1/5 Divided By 6 As A Fraction
News Co
May 08, 2025 · 5 min read
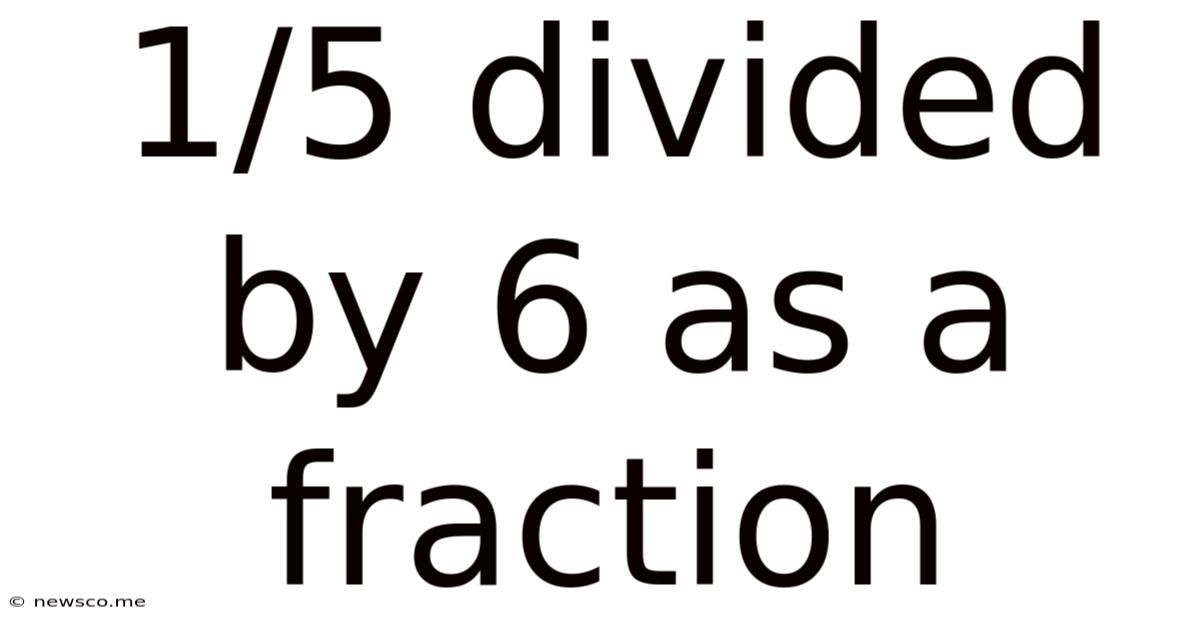
Table of Contents
1/5 Divided by 6: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it opens doors to more complex mathematical concepts. This comprehensive guide will walk you through the process of dividing the fraction 1/5 by the whole number 6, explaining the steps involved and providing practical examples. We'll also explore the underlying principles and delve into some common mistakes to avoid. By the end, you'll confidently tackle similar problems and solidify your understanding of fraction arithmetic.
Understanding Fraction Division
Before we dive into the specific problem of 1/5 divided by 6, let's review the fundamentals of fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
The key concept to remember is: Dividing by a number is the same as multiplying by its reciprocal.
This rule applies whether you're dividing a fraction by a fraction, a fraction by a whole number, or a whole number by a fraction.
Solving 1/5 Divided by 6
Now, let's tackle the problem at hand: 1/5 ÷ 6.
First, we need to rewrite the whole number 6 as a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 6 can be written as 6/1.
Our problem now becomes: 1/5 ÷ 6/1
Next, we apply the rule of fraction division: we change the division sign to a multiplication sign and flip the second fraction (find its reciprocal). The reciprocal of 6/1 is 1/6.
So, our problem transforms into: 1/5 × 1/6
Now, we simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 1) / (5 × 6) = 1/30
Therefore, 1/5 divided by 6 is equal to 1/30.
Visualizing the Problem
Imagine you have a pizza cut into 5 equal slices. You have 1 slice (1/5 of the pizza). You want to divide this single slice among 6 people. Each person will receive a much smaller portion of the original pizza. This smaller portion represents 1/30 of the whole pizza.
Step-by-Step Breakdown: A Practical Approach
Let's break down the solution methodically, highlighting crucial steps:
- Rewrite the whole number as a fraction: 6 becomes 6/1.
- Convert division to multiplication: Change the division sign (÷) to a multiplication sign (×).
- Find the reciprocal of the second fraction: Flip the second fraction, 6/1, to become 1/6.
- Multiply the fractions: Multiply the numerators together (1 x 1 = 1) and the denominators together (5 x 6 = 30).
- Simplify the fraction (if possible): In this case, 1/30 is already in its simplest form because 1 and 30 have no common factors other than 1.
Common Mistakes to Avoid
Several common mistakes can occur when dividing fractions. Let's address some of them:
- Forgetting to find the reciprocal: This is perhaps the most common mistake. Remember, you must flip the second fraction before multiplying. Simply multiplying the fractions without finding the reciprocal will yield an incorrect answer.
- Incorrectly multiplying or dividing the numerators and denominators: Pay close attention to the arithmetic. Double-check your multiplication and ensure you're correctly multiplying the numerators and the denominators.
- Not simplifying the fraction: Always simplify your final answer to its lowest terms. This makes the answer easier to understand and is considered good mathematical practice.
Advanced Applications and Extensions
The concept of dividing fractions extends far beyond simple problems like 1/5 ÷ 6. Understanding this fundamental principle lays the groundwork for more complex scenarios, including:
- Dividing fractions by fractions: The same principles apply. Convert the division to multiplication and find the reciprocal of the second fraction.
- Dividing mixed numbers: Convert mixed numbers (like 2 1/2) into improper fractions (like 5/2) before applying the division rules.
- Solving real-world problems: Many real-world problems, such as sharing resources or calculating proportions, require dividing fractions.
Real-World Examples
Let's explore some real-world applications to solidify your understanding:
- Baking: You have 1/5 of a cup of sugar and need to divide it equally among 6 cupcakes. How much sugar goes into each cupcake? The answer, 1/30 of a cup, is obtained by dividing 1/5 by 6.
- Sharing Resources: Imagine you have 1/5 of a pizza and you need to share it among 6 friends. Each friend gets 1/30 of the pizza.
- Construction: If a construction project requires 1/5 of a ton of cement and you want to divide the work into 6 days, you'd use 1/30 of a ton of cement per day.
Practice Problems
To reinforce your learning, try solving these problems:
- 2/3 ÷ 4
- 3/7 ÷ 5
- 1/2 ÷ 3/4
- 2 1/3 ÷ 2
These exercises will help you internalize the process and build your confidence in dividing fractions. Remember to break each problem down into steps, following the procedure outlined above.
Conclusion
Dividing fractions, even a seemingly simple problem like 1/5 ÷ 6, involves a crucial understanding of reciprocals and the transformation of division into multiplication. By mastering this fundamental concept, you'll develop a strong foundation for tackling more complex mathematical challenges and real-world applications. Remember to practice regularly and review the steps outlined in this guide to ensure you can confidently solve any fraction division problem. The more you practice, the easier it will become, transforming what may seem challenging into a straightforward process. Through practice and understanding, conquering fractions will become second nature.
Latest Posts
Latest Posts
-
X 5 X 3 1 X 2
May 09, 2025
-
3 Divided By 8 In Fraction
May 09, 2025
-
Range Of Stem And Leaf Plot
May 09, 2025
-
Can A Given Point Be In Two Lines
May 09, 2025
-
How To Get Rid Of Fraction Exponents
May 09, 2025
Related Post
Thank you for visiting our website which covers about 1/5 Divided By 6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.