1 And 1/6 As A Decimal
News Co
May 07, 2025 · 5 min read
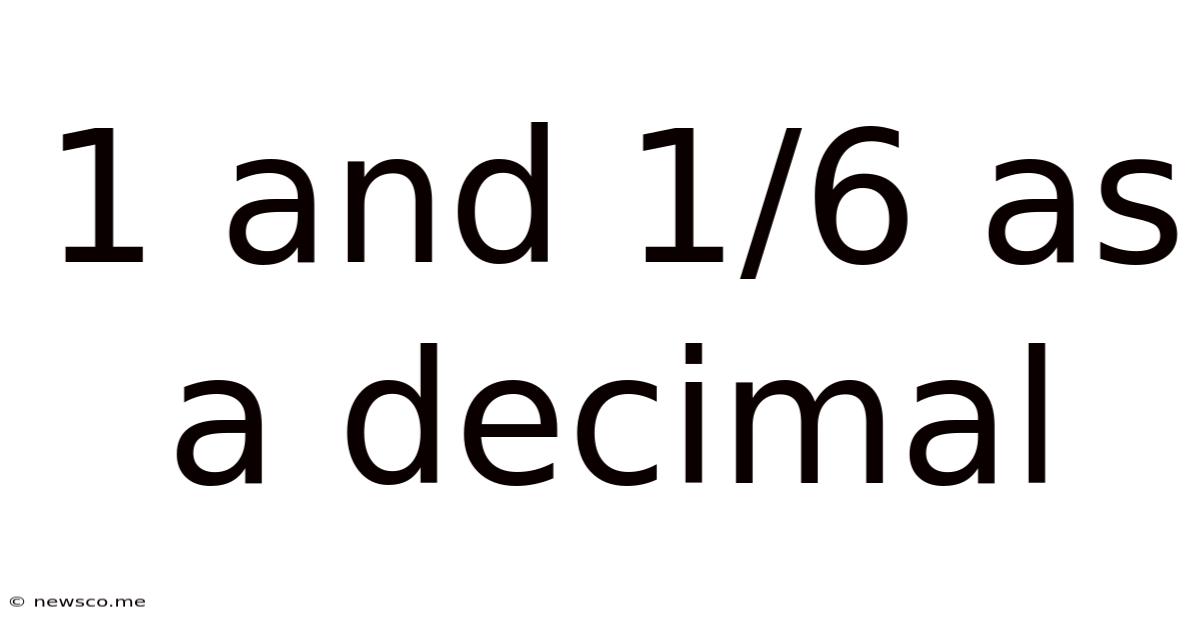
Table of Contents
1 and 1/6 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications in science, engineering, and everyday life. This comprehensive guide delves into the process of converting the mixed number 1 and 1/6 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying concepts. We'll also touch upon the broader implications of decimal representation and its significance in numerical calculations.
Understanding Fractions and Decimals
Before diving into the conversion, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/6, 1 is the numerator and 6 is the denominator. This means we have one part out of six equal parts.
A decimal, on the other hand, represents a number using a base-10 system. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, and so on). For instance, 0.5 represents five-tenths, and 0.25 represents twenty-five hundredths.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator by the denominator. In our case, we need to convert 1 and 1/6 to an improper fraction first.
Converting Mixed Numbers to Improper Fractions
A mixed number, like 1 and 1/6, combines a whole number (1) and a fraction (1/6). To convert it to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 6 = 6
- Add the numerator to the result: 6 + 1 = 7
- Keep the same denominator: The denominator remains 6.
Therefore, 1 and 1/6 is equivalent to the improper fraction 7/6.
Performing Long Division
Now, we perform the long division: 7 ÷ 6.
1.1666...
6 | 7.0000
-6
10
-6
40
-36
40
-36
40
-36
4...
As you can see, the division results in a repeating decimal: 1.1666... The digit 6 repeats infinitely.
Method 2: Using a Calculator
A simpler, quicker method involves using a calculator. Simply enter 7 ÷ 6 and the calculator will directly provide the decimal equivalent: 1.166666... Calculators typically display a limited number of decimal places, but the result is still the same repeating decimal.
Understanding Repeating Decimals
The result of converting 1 and 1/6 to a decimal is a repeating decimal, also known as a recurring decimal. A repeating decimal is a decimal that has a sequence of digits that repeats indefinitely. We often represent repeating decimals using a bar over the repeating digits. In our case, it's represented as 1.1̅6̅. The bar indicates that the digits "16" repeat infinitely.
Representing Repeating Decimals
There are several ways to represent repeating decimals:
- Using a bar: 1.1̅6̅ is the most common and concise method.
- Using ellipses: 1.1666... indicates that the 6s continue indefinitely.
- Using fractional form: While we started with a fraction, it's crucial to remember that this is the most precise representation of the number.
Significance of Decimal Representation
The decimal representation of a number is crucial for several reasons:
- Ease of Comparison: Decimals allow for easier comparison of numbers compared to fractions, especially when dealing with multiple fractions with different denominators.
- Computational Efficiency: Many calculations are more efficiently performed using decimals, particularly with calculators and computers.
- Real-World Applications: Decimals are extensively used in various fields, including finance, engineering, science, and everyday measurements (like length, weight, and volume).
Applications of 1 and 1/6 (1.1̅6̅)
The decimal representation of 1 and 1/6, 1.1̅6̅, has practical applications in various contexts:
- Measurement: Imagine measuring a length of 1 and 1/6 meters. The decimal form (1.1666...) makes it easier to work with in calculations involving other measurements.
- Finance: Calculating interest or portions of investments might involve fractions like 1 and 1/6. The decimal equivalent simplifies the calculations.
- Engineering: Many engineering calculations rely on precise decimal representations for accurate results.
- Data Analysis: Data sets often involve fractions, and converting them to decimals facilitates statistical analysis and visualizations.
Decimal Accuracy and Rounding
While repeating decimals extend infinitely, in practical applications, we often need to round them to a certain number of decimal places. Rounding depends on the level of accuracy required:
- Rounding to one decimal place: 1.2
- Rounding to two decimal places: 1.17
- Rounding to three decimal places: 1.167
Rounding introduces a small degree of error, but it is often acceptable depending on the context and the level of precision required.
Beyond the Basics: Further Exploration
Understanding the conversion of fractions to decimals opens up avenues for exploring more complex concepts:
- Rational and Irrational Numbers: The fraction 1 and 1/6 represents a rational number (a number that can be expressed as a fraction of two integers). Its decimal representation, though repeating, is still a rational number. In contrast, irrational numbers, like π (pi), have non-repeating, non-terminating decimal expansions.
- Significant Figures and Scientific Notation: In scientific applications, significant figures and scientific notation are used to express numbers with a high degree of precision, often in decimal form.
- Computer Representation of Numbers: Computers store and process numbers using binary representations, but they often handle decimal calculations through sophisticated algorithms and data structures.
Conclusion
Converting 1 and 1/6 to its decimal equivalent, 1.1̅6̅, is a straightforward process using long division or a calculator. Understanding the concept of repeating decimals and their representation is crucial for various mathematical applications. The decimal form simplifies comparisons and computations, making it a valuable tool in numerous fields. Remember to choose the appropriate level of decimal precision based on the context of your application, and be mindful of the slight error introduced by rounding. The ability to confidently convert between fractions and decimals is a fundamental skill that opens doors to more advanced mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
1 4 On A Number Line From 0 To 1
May 08, 2025
-
Find The Roots Of A Complex Number
May 08, 2025
-
Which Of The Following Expressions Is A Polynomial
May 08, 2025
-
How To Find Ratio Of Surface Area
May 08, 2025
-
Given 1 And 2 Are Supplements
May 08, 2025
Related Post
Thank you for visiting our website which covers about 1 And 1/6 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.