1 Divided By 1 3 As A Fraction
News Co
Apr 03, 2025 · 5 min read
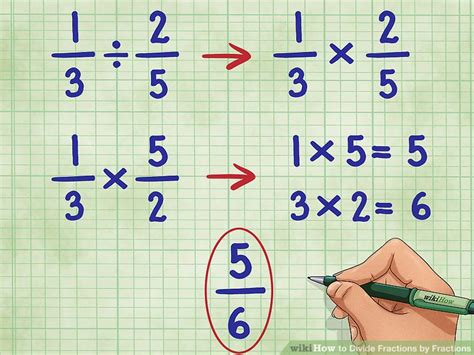
Table of Contents
1 Divided by 1 ⅓ as a Fraction: A Comprehensive Guide
Understanding fractions and how to perform operations with them is a cornerstone of mathematics. This seemingly simple problem – 1 divided by 1 ⅓ – provides a valuable opportunity to explore various methods for solving division problems involving mixed numbers and to solidify your understanding of fractional arithmetic. This comprehensive guide will walk you through the process step-by-step, explaining the underlying principles and offering alternative approaches.
Understanding the Problem: 1 ÷ 1⅓
Before diving into the solution, let's clarify what the problem entails. We are asked to find the result of dividing 1 by the mixed number 1⅓. Remember that a mixed number combines a whole number and a fraction (like 1⅓). To solve this, we need to convert the mixed number into an improper fraction and then apply the rules of fraction division.
Converting Mixed Numbers to Improper Fractions
A mixed number, like 1⅓, represents a whole number plus a fraction. To convert it to an improper fraction (where the numerator is larger than the denominator), we follow these steps:
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: 3
Therefore, 1⅓ converts to the improper fraction ⁴⁄₃.
Method 1: Dividing Fractions
Now that we've converted the mixed number, our problem becomes 1 ÷ ⁴⁄₃. Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down.
- Find the reciprocal of ⁴⁄₃: The reciprocal of ⁴⁄₃ is ³⁄₄.
- Rewrite the division as multiplication: 1 x ³⁄₄ = ³⁄₄
Therefore, 1 divided by 1⅓ is equal to ¾.
Method 2: Using Decimal Representation
Another approach involves converting the mixed number to a decimal and then performing the division.
- Convert 1⅓ to a decimal: 1⅓ is equal to 1.333... (repeating decimal).
- Perform the division: 1 ÷ 1.333... This calculation will result in approximately 0.75.
While this method provides a close approximation, it's important to note that the repeating decimal introduces a slight margin of error. The fraction method provides a more precise and exact answer.
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for those who prefer a more intuitive approach. Imagine you have a whole pizza (representing the number 1). You want to divide this pizza into portions, each the size of 1⅓ pizzas. How many of these larger portions fit into a single pizza? Clearly, you can't fit even one complete 1⅓ pizza portion into a single pizza. This visual understanding reinforces that the answer will be a fraction less than 1.
Practical Applications and Real-World Examples
Understanding division with mixed numbers isn't just an academic exercise. It's crucial in various real-world scenarios:
-
Baking and Cooking: Recipes often call for fractions and mixed numbers of ingredients. Calculating the correct amount when scaling a recipe up or down requires proficiency in fractional arithmetic. For instance, if a recipe requires 1⅓ cups of flour and you want to halve the recipe, you'd need to calculate ½ x ⁴⁄₃ to determine the new flour amount.
-
Construction and Engineering: Precision is paramount in construction and engineering. Dividing lengths, materials, or measurements often involves fractions and mixed numbers. For example, cutting a board of a certain length into smaller pieces requires understanding fractional division.
-
Sewing and Tailoring: Pattern adjustments and fabric calculations commonly involve fractions and mixed numbers. Determining the required amount of fabric for a project or adjusting pattern pieces demands precise fractional arithmetic.
-
Finance and Budgeting: Dealing with portions of money or calculating interest often involves fractions and decimals. Understanding these concepts helps in managing personal finances and investments.
Expanding on Fractional Arithmetic: Beyond the Basics
The solution to 1 ÷ 1⅓ serves as a foundation for exploring more complex fractional operations:
-
Multiplication of Fractions: We saw how division is related to multiplication of reciprocals. Mastering fraction multiplication is essential for more advanced problems.
-
Addition and Subtraction of Fractions: Adding and subtracting fractions require finding a common denominator. This skill is critical when dealing with more complicated mixed numbers and fractions.
-
Complex Fractions: Complex fractions involve fractions within fractions. Knowing how to simplify these can help solve seemingly daunting problems.
-
Fractions and Decimals: Converting between fractions and decimals is a valuable skill that simplifies calculations in various contexts.
Troubleshooting Common Mistakes
When dealing with fractions and mixed numbers, certain errors are common:
-
Incorrect Conversion of Mixed Numbers: Failure to convert mixed numbers accurately to improper fractions is a significant source of error. Always double-check your conversions.
-
Mistaking Reciprocal: Incorrectly identifying the reciprocal of a fraction can lead to an entirely wrong answer. Remember to flip the numerator and the denominator.
-
Improper Multiplication or Division: Errors in the multiplication or division of fractions can occur. Pay close attention to the signs and operations.
-
Oversimplification or Insufficient Simplification: Make sure to simplify the resulting fraction to its lowest terms. Leaving it in an unsimplified form may not be considered a fully correct answer.
Conclusion: Mastering Fractional Division
The seemingly simple problem of 1 divided by 1⅓ offers a rich opportunity to practice and solidify your understanding of fractional arithmetic. Mastering the techniques outlined here – converting mixed numbers, using reciprocals, and carefully performing the calculations – is vital for success in various mathematical and real-world applications. Regular practice and a focus on accuracy will build confidence and proficiency in working with fractions, leading to a deeper understanding of mathematical concepts and their applications. By understanding the various methods and potential pitfalls, you can confidently tackle similar problems and expand your mathematical abilities. Remember that consistent practice is key to mastering fractions and enhancing your overall mathematical skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.