1 Divided By 1 3 In Fraction
News Co
Apr 15, 2025 · 4 min read
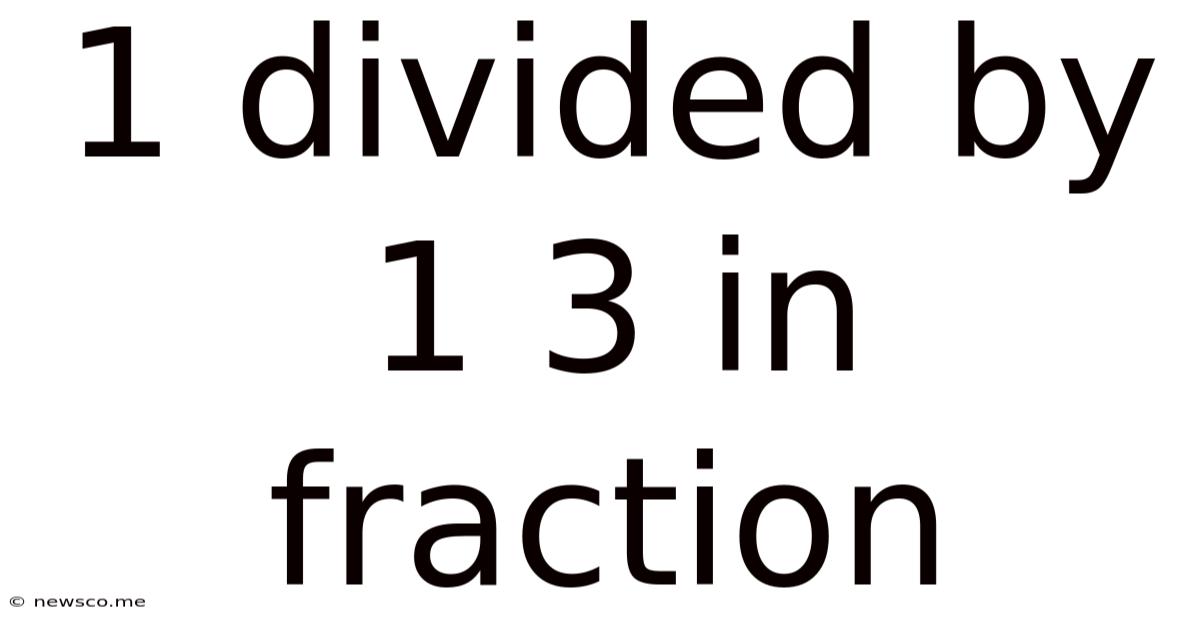
Table of Contents
1 Divided by 1 ⅓: A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting, but with a systematic approach, it becomes manageable and even intuitive. This article delves deep into the process of dividing 1 by the mixed number 1 ⅓, explaining the steps, the underlying principles, and providing various methods to solve this and similar problems. We'll explore why this seemingly simple calculation holds significant importance in various mathematical contexts.
Understanding the Problem: 1 ÷ 1 ⅓
The problem, 1 ÷ 1 ⅓, asks us to determine how many times the mixed number 1 ⅓ goes into 1. This is fundamentally a division problem involving fractions. To solve it effectively, we need to convert the mixed number into an improper fraction and then apply the rules of fraction division.
Mixed Numbers and Improper Fractions: A Quick Refresher
A mixed number combines a whole number and a fraction (e.g., 1 ⅓). An improper fraction has a numerator larger than or equal to its denominator (e.g., 4/3). Converting between the two is crucial for fraction division.
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator of the fraction.
- Keep the same denominator.
For 1 ⅓:
- 1 (whole number) * 3 (denominator) = 3
- 3 + 1 (numerator) = 4
- The improper fraction is 4/3.
Therefore, our problem becomes: 1 ÷ 4/3
Methods for Dividing Fractions
There are several ways to approach dividing fractions. We'll explore two primary methods: the reciprocal method and the common denominator method.
Method 1: The Reciprocal Method (The Most Common and Easiest Method)
This is the most commonly taught method. It involves these steps:
-
Convert any mixed numbers to improper fractions: As shown above, 1 ⅓ becomes 4/3. The number 1 can be written as the fraction 1/1.
-
Change the division to multiplication by using the reciprocal of the second fraction: The reciprocal of a fraction is obtained by swapping the numerator and the denominator. The reciprocal of 4/3 is 3/4. So, our problem becomes: (1/1) * (3/4).
-
Multiply the numerators and multiply the denominators: (1 * 3) / (1 * 4) = 3/4
Therefore, 1 ÷ 1 ⅓ = ¾
Method 2: The Common Denominator Method (A Less Common, but Equally Valid Method)
This method provides a more intuitive understanding of fraction division, especially for those who find the reciprocal method less clear.
-
Convert mixed numbers to improper fractions: Again, 1 ⅓ becomes 4/3, and 1 becomes 1/1.
-
Find a common denominator for both fractions: In this case, the common denominator is 3.
-
Rewrite the fractions with the common denominator: 1/1 becomes 3/3.
-
Divide the numerators: (3/3) ÷ (4/3) = 3 ÷ 4 = ¾
This method visually demonstrates how many times 4/3 fits into 3/3.
Why Understanding Fraction Division is Important
Mastering fraction division isn't just about solving textbook problems; it's a fundamental skill with wide-ranging applications in:
-
Cooking and Baking: Scaling recipes up or down often requires dividing fractions. For example, if a recipe calls for 1 ⅓ cups of flour and you want to halve the recipe, you'll need to divide 1 ⅓ by 2.
-
Construction and Engineering: Precise measurements are crucial, and calculations often involve fractions and mixed numbers. Dividing fractions accurately ensures correct proportions and prevents errors.
-
Sewing and Tailoring: Cutting fabric to the right dimensions relies on accurate calculations, frequently involving fractions.
-
Data Analysis and Statistics: Many statistical calculations involve fractions and ratios, often requiring division operations.
-
Finance and Accounting: Understanding fractions is vital for handling proportions, percentages, and ratios in financial calculations.
-
Everyday Life: Numerous situations involve sharing resources or dividing quantities, which necessitates understanding how to divide fractions.
Advanced Applications and Extensions
The principles used to solve 1 ÷ 1 ⅓ can be extended to more complex problems involving:
-
Dividing larger mixed numbers: The same steps of converting to improper fractions and using the reciprocal method (or common denominator method) apply.
-
Dividing fractions by whole numbers: The whole number can be written as a fraction with a denominator of 1.
-
Dividing decimals by fractions: Convert the decimal to a fraction, then apply the same fraction division methods.
-
Solving word problems involving fraction division: Practice translating word problems into mathematical expressions, then use the appropriate methods to solve them.
Practical Exercises
To solidify your understanding, try these problems:
- 2 ÷ 1 ½
- 3 ½ ÷ 2 ⅓
- 0.75 ÷ ¾
- A recipe calls for 2 ⅔ cups of sugar. If you want to make only half the recipe, how much sugar should you use?
Solving these problems will enhance your skills and confidence in handling fraction division.
Conclusion: Mastering the Art of Fraction Division
Dividing fractions, particularly involving mixed numbers, might seem challenging at first glance. However, by understanding the underlying principles, mastering the conversion between mixed numbers and improper fractions, and choosing an appropriate method (reciprocal or common denominator), you can tackle these problems efficiently and accurately. The ability to perform these calculations is an invaluable skill applicable to numerous aspects of life, from everyday tasks to more specialized fields. Remember to practice consistently to improve your proficiency and build confidence in your mathematical abilities. With dedicated practice, fraction division will become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 3 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.