1 Out Of 16 As A Percentage
News Co
Mar 20, 2025 · 5 min read
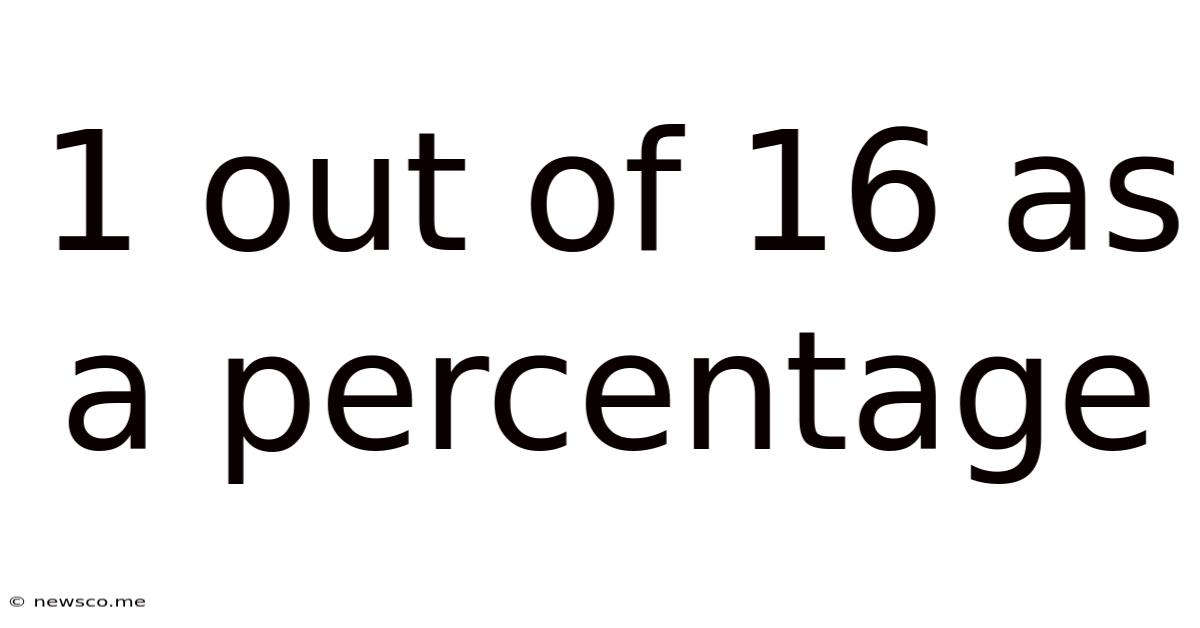
Table of Contents
1 out of 16 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill applicable across various aspects of life, from everyday budgeting to complex financial analyses. This comprehensive guide will delve deep into the calculation of "1 out of 16 as a percentage," explaining the process, exploring different calculation methods, and providing practical examples to solidify your understanding. We'll also explore the broader context of fractions and percentages, equipping you with the tools to tackle similar problems with confidence.
Understanding Fractions and Percentages
Before diving into the specific calculation, let's establish a clear understanding of the core concepts involved: fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts. In our case, "1 out of 16" is represented as the fraction 1/16.
Percentages: A percentage is a way of expressing a fraction as a portion of 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 1 out of 16 as a Percentage: Method 1 - Direct Conversion
The most straightforward method to convert 1/16 to a percentage involves a simple two-step process:
Step 1: Convert the fraction to a decimal.
To do this, divide the numerator (1) by the denominator (16):
1 ÷ 16 = 0.0625
Step 2: Convert the decimal to a percentage.
Multiply the decimal by 100 and add the percentage symbol (%):
0.0625 × 100 = 6.25%
Therefore, 1 out of 16 is equal to 6.25%.
Calculating 1 out of 16 as a Percentage: Method 2 - Using Proportions
This method utilizes the concept of proportions to solve the problem. We can set up a proportion to find the equivalent percentage:
1/16 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
16x = 100
x = 100/16
x = 6.25
Therefore, 1 out of 16 is 6.25%. This method reinforces the understanding that percentages are essentially fractions with a denominator of 100.
Practical Applications and Real-World Examples
Understanding how to calculate percentages from fractions has numerous practical applications in various fields:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves working with fractions and percentages. For example, if a company reports a profit of 1 out of every 16 sales, this means their profit margin is 6.25%.
- Statistics: Representing data in terms of percentages allows for easier comparison and interpretation. If a survey shows that 1 out of 16 respondents prefer a particular product, this represents a 6.25% preference rate.
- Probability: Calculating probabilities often involves fractions. Expressing these probabilities as percentages makes them easier to understand. For instance, if the probability of winning a game is 1 out of 16, the probability of winning is 6.25%.
- Everyday Life: Calculating discounts in shops, understanding tip percentages in restaurants, or determining the proportion of ingredients in recipes all involve percentage calculations stemming from fractional representations.
Expanding on Fraction to Percentage Conversions
While we've focused on 1/16, the methods described can be applied to any fraction. Let's explore a few more examples:
- 1/4 as a Percentage: 1 ÷ 4 = 0.25; 0.25 × 100 = 25%
- 3/8 as a Percentage: 3 ÷ 8 = 0.375; 0.375 × 100 = 37.5%
- 5/12 as a Percentage: 5 ÷ 12 ≈ 0.4167; 0.4167 × 100 ≈ 41.67%
Dealing with More Complex Fractions
The principles remain the same even when dealing with more complex fractions. For instance, converting a fraction like 15/64 to a percentage:
15 ÷ 64 ≈ 0.2344; 0.2344 × 100 ≈ 23.44%
Remember to round your answers appropriately depending on the level of precision required.
The Importance of Accuracy and Precision
When working with percentages, accuracy is paramount. Rounding errors, even small ones, can accumulate and lead to significant discrepancies in calculations, especially in financial or scientific contexts. Use calculators or software to ensure accuracy, and round your final answer to the appropriate number of decimal places based on the context of the problem.
Utilizing Online Calculators and Tools
Various online calculators and tools are available to aid in percentage calculations. These tools can be particularly helpful for complex fractions or when speed and accuracy are crucial. However, understanding the underlying principles remains vital, as it allows you to critically evaluate the results provided by these tools.
Troubleshooting Common Errors
Some common errors encountered when converting fractions to percentages include:
- Incorrect division: Ensure you divide the numerator by the denominator correctly.
- Forgetting to multiply by 100: Remember that the decimal result needs to be multiplied by 100 to express it as a percentage.
- Rounding errors: Pay attention to the level of precision required and round your answer appropriately.
Conclusion: Mastering Fraction to Percentage Conversions
Understanding how to convert fractions to percentages is a valuable skill with far-reaching applications. This guide has provided a thorough explanation of how to convert "1 out of 16 as a percentage," showcasing different methods and highlighting the importance of accuracy and precision. By mastering this fundamental skill, you will be better equipped to tackle various challenges across diverse fields, from everyday calculations to more complex quantitative analyses. Remember that consistent practice and attention to detail are key to achieving proficiency in this area. The ability to accurately and efficiently convert fractions to percentages is a cornerstone of numerical literacy and a valuable asset in numerous contexts.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 1 Out Of 16 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.