1 Raised To The Power Of 5
News Co
Apr 23, 2025 · 5 min read
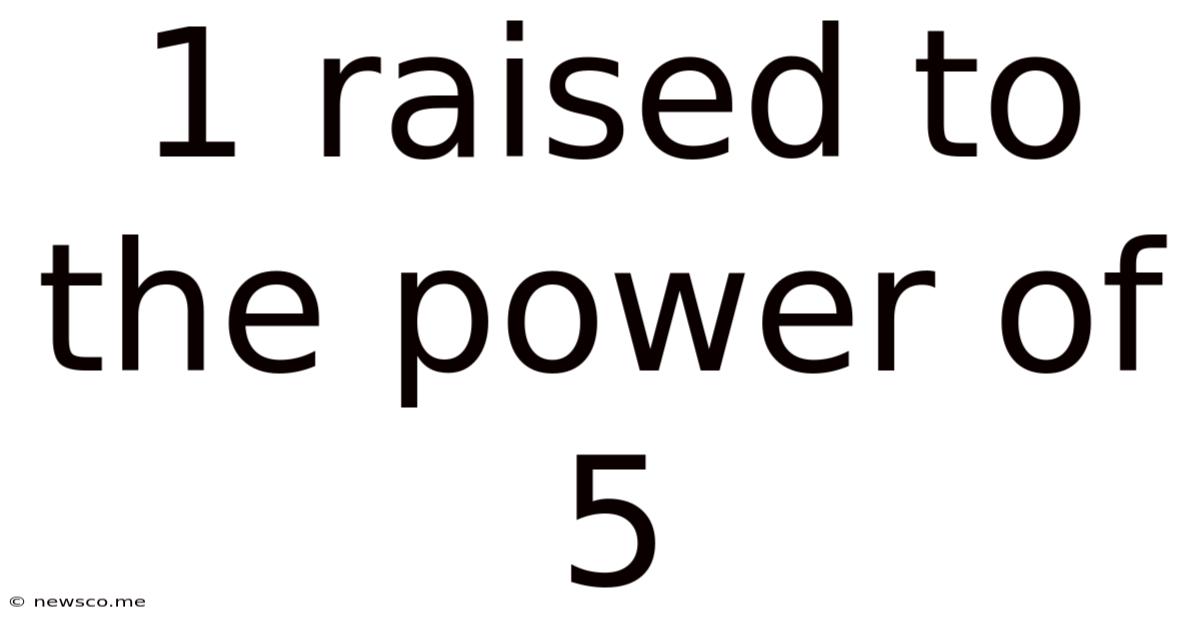
Table of Contents
1 Raised to the Power of 5: A Deep Dive into Exponents and Their Implications
The seemingly simple expression "1 raised to the power of 5," or 1⁵, might appear trivial at first glance. However, exploring this seemingly basic mathematical concept reveals deeper insights into the fundamental properties of exponents and their wide-ranging applications across various fields. This article delves into the intricacies of this expression, examining its calculation, its significance in different mathematical contexts, and its broader implications in areas like computer science, finance, and beyond.
Understanding Exponents: A Foundation for 1⁵
Before diving into the specifics of 1⁵, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the general form a<sup>n</sup>, 'a' represents the base, and 'n' represents the exponent. For instance, 2³ (2 raised to the power of 3) means 2 × 2 × 2 = 8.
The Uniqueness of the Number 1 as a Base
The number 1 possesses a unique property when used as a base in exponential expressions. Regardless of the exponent's value (whether positive, negative, or zero), 1 raised to any power always equals 1. This is because multiplying 1 by itself any number of times always results in 1.
Calculating 1⁵: A Straightforward Result
Calculating 1⁵ is straightforward. It simply means multiplying 1 by itself five times: 1 × 1 × 1 × 1 × 1 = 1. The result, unsurprisingly, is 1. This consistent outcome underscores the unique behavior of 1 as a base in exponential functions.
Expanding the Scope: Exploring Different Exponents with Base 1
While 1⁵ is a simple case, let's explore other exponents with a base of 1 to further illustrate this fundamental property:
- 1⁰ (1 raised to the power of 0): Any non-zero number raised to the power of 0 equals 1. This is a crucial rule in algebra and is consistent with the pattern of exponents.
- 1¹ (1 raised to the power of 1): This is simply 1, as any number raised to the power of 1 is the number itself.
- 1⁻¹ (1 raised to the power of -1): This is equivalent to 1/1, which equals 1. Negative exponents represent reciprocals.
- 1<sup>n</sup> (1 raised to the power of n): Where 'n' can be any real number, the result will always be 1. This includes fractional exponents, irrational exponents, and even complex exponents.
This consistent behavior of 1 as a base highlights its fundamental role in mathematics. It serves as a neutral element in multiplication, and this neutrality extends to its exponential behavior.
Beyond Simple Calculation: The Significance of 1⁵ in Mathematical Contexts
The seemingly simple result of 1⁵ has significant implications within broader mathematical frameworks:
Identity Element in Group Theory
In abstract algebra, particularly in group theory, the number 1 acts as the identity element under multiplication. This means that multiplying any element in the group by 1 leaves the element unchanged. This concept extends to exponential operations, where 1 raised to any power maintains its identity as 1.
Applications in Polynomial Expansions
1⁵, and more generally, 1 raised to any power, plays a role in simplifying polynomial expansions. Consider the binomial theorem; the terms involving powers of 1 often simplify the calculation significantly.
Implications for Limits and Calculus
When considering limits of functions or derivatives in calculus, the constant value of 1 raised to any power can lead to simplifications and predictable results. This consistency makes it a useful tool in advanced mathematical analysis.
1⁵ and its Applications in Real-World Scenarios
While 1⁵ itself might seem inconsequential, the underlying principle of a base raised to a power has profound implications across numerous fields:
Computer Science and Binary Systems
In computer science, binary systems rely on powers of 2 (e.g., 2⁰, 2¹, 2², etc.). However, the principle of exponents is fundamental. The concept of a base raised to a power is crucial in understanding data representation, memory addressing, and algorithmic complexity.
Financial Modeling and Compound Interest
In finance, compound interest calculations involve exponents. While the base might not always be 1, the concept is fundamentally linked. Understanding exponential growth (or decay) is essential for financial planning, investment strategies, and risk assessment. Although 1⁵ doesn't directly appear in these calculations, the principle of exponentiation is central to the mathematical models used.
Physics and Exponential Decay
In physics, exponential decay describes processes like radioactive decay and the decrease in amplitude of damped oscillations. The exponent helps model the rate of decay. While the base might represent a decay factor different from 1, the fundamental concept remains relevant.
Biology and Population Growth
Exponential growth models are used to represent population growth in biology. While the base usually represents a growth factor greater than 1, the understanding of exponents is critical in making predictions and analyzing population dynamics.
Conclusion: The Unsung Significance of 1⁵
While the calculation of 1⁵ yields the seemingly trivial result of 1, its implications are far-reaching. This simple expression acts as a gateway to understanding the fundamental properties of exponents, their behavior with different bases, and their widespread applications in various scientific and mathematical disciplines. The consistent behavior of 1 as a base underscores its unique role as an identity element, simplifying calculations and providing a foundation for more complex mathematical concepts. From computer science algorithms to financial modeling, the underlying principles of exponentiation, even with seemingly simple expressions like 1⁵, remain crucial for a deep understanding of numerous real-world phenomena. The seemingly simple calculation highlights the power of fundamental mathematical principles and their vast and often unexpected impact on diverse fields of study.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 Raised To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.