1 Sin X 1 Sin X
News Co
Apr 10, 2025 · 5 min read
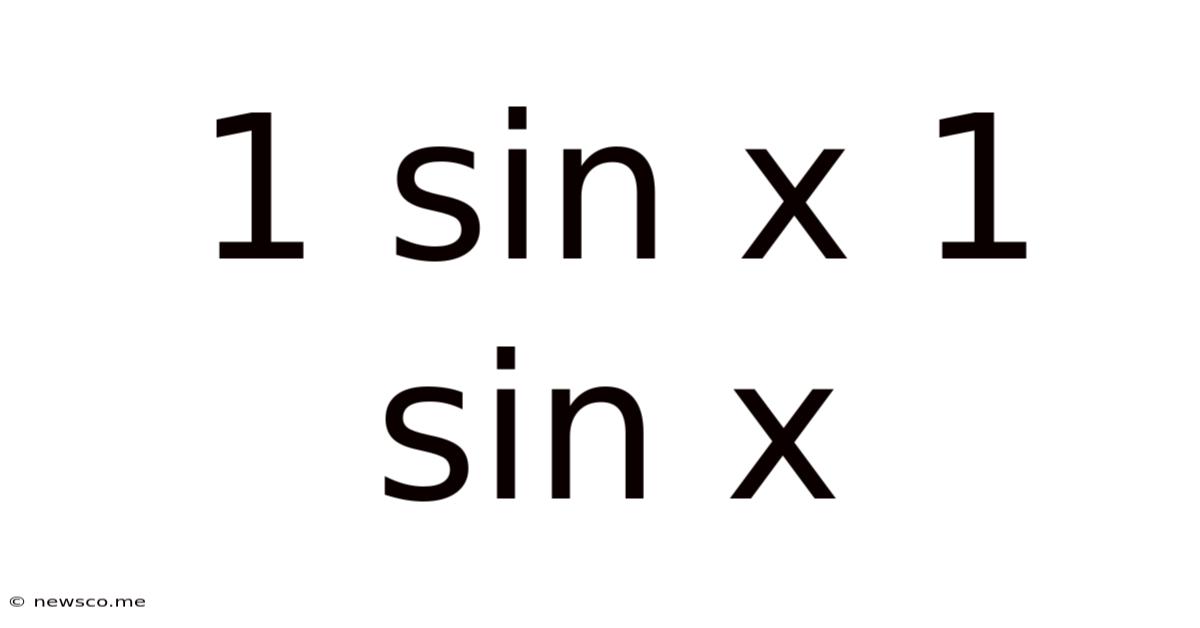
Table of Contents
Decoding 1 sin x 1 sin x: A Deep Dive into Trigonometric Identities and Applications
The expression "1 sin x 1 sin x" isn't a standard mathematical notation. It's likely a typo or a shorthand representation. However, it hints at explorations within trigonometry, specifically involving the sine function. This article will delve into various interpretations of this ambiguous expression, exploring related trigonometric identities, their applications, and practical examples. We'll clarify common misunderstandings and provide a comprehensive understanding of how sine functions behave in different contexts.
Understanding the Sine Function: A Foundation
Before tackling potential interpretations of "1 sin x 1 sin x," let's establish a firm grasp of the sine function itself. In a right-angled triangle, the sine of an angle (often denoted as sin x, where x is the angle in degrees or radians) is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Key Properties of the Sine Function:
- Periodicity: The sine function is periodic, meaning it repeats its values at regular intervals. Its period is 2π radians (or 360 degrees). This means sin(x + 2π) = sin(x) for any value of x.
- Range: The output of the sine function (its range) is bounded between -1 and 1, inclusive. That is, -1 ≤ sin(x) ≤ 1.
- Domain: The sine function is defined for all real numbers. You can input any real number as x, and the function will produce a corresponding output.
- Odd Function: The sine function is an odd function, meaning sin(-x) = -sin(x). This symmetry is reflected in its graph.
- Relationship to Cosine: The sine and cosine functions are closely related through the identity sin²(x) + cos²(x) = 1. This fundamental identity underpins many trigonometric manipulations.
Potential Interpretations of "1 sin x 1 sin x"
Given the ambiguity of the expression, we'll consider several possible interpretations, analyzing each carefully:
1. A Typographical Error: The most likely scenario is that "1 sin x 1 sin x" is a typo. It could represent one of the following:
-
(1 + sin x)(1 - sin x): This represents the difference of squares. Using the identity a² - b² = (a + b)(a - b), where a = 1 and b = sin x, we can simplify this expression to: 1 - sin²x = cos²x (using the Pythagorean identity mentioned earlier). This is a very important identity used extensively in calculus, trigonometry, and physics.
-
1 + sin x + 1 - sin x: This simplifies to 2, a constant value independent of x. This interpretation is straightforward but less likely given the context of trigonometric manipulations.
-
1/(sin x) + 1/(sin x): This expression can be simplified to 2/sin x or 2csc x (where csc x is the cosecant function, the reciprocal of sine). This representation is valid and meaningful in various trigonometric problems.
2. A Representation of Amplitude Modulation: In signal processing and electronics, expressions similar to this could represent amplitude modulation. Here, '1' might represent a carrier signal, and 'sin x' a modulating signal. The combined expression then describes a wave whose amplitude varies according to the sine wave.
3. A Component of a Larger Equation: It's possible that "1 sin x 1 sin x" is part of a larger, more complex equation. The context is crucial in determining its meaning. For example, it could be:
- Part of a differential equation.
- A term in a Fourier series.
- Part of a physics formula describing wave phenomena.
Applications of Trigonometric Identities
Understanding and manipulating trigonometric identities is crucial in various fields:
1. Calculus: Trigonometric identities are frequently used in integral and differential calculus to simplify complex expressions. For example, the identity cos²x = (1 + cos 2x)/2 is crucial for evaluating integrals involving cosine squared.
2. Physics: Trigonometry is fundamental to physics, particularly in mechanics, optics, and electromagnetism. It's used to model oscillations, waves, and rotations. For instance, understanding the sine wave is essential in analyzing simple harmonic motion.
3. Engineering: Trigonometric functions and identities are critical in engineering disciplines such as civil, mechanical, and electrical engineering. They are used to analyze stresses and strains in structures, design circuits, and model rotating machinery.
4. Computer Graphics and Game Development: Trigonometric functions are indispensable in creating realistic computer graphics and video games. They are used to render three-dimensional objects, calculate rotations, and model physics simulations.
5. Navigation and Surveying: Trigonometric functions are utilized in navigation and surveying to determine distances and locations using angles and measurements.
Advanced Trigonometric Concepts
Let's explore some more advanced concepts relevant to understanding the nuances of sine functions:
1. Inverse Sine Function (arcsin): The inverse sine function, denoted as arcsin(x) or sin⁻¹(x), finds the angle whose sine is x. It's important to note that the inverse sine function has a restricted range to avoid multiple solutions.
2. Double and Triple Angle Formulas: These identities express trigonometric functions of multiple angles in terms of functions of the single angle. For example, sin(2x) = 2sin(x)cos(x) and sin(3x) = 3sin(x) - 4sin³(x).
3. Sum-to-Product and Product-to-Sum Formulas: These identities transform sums and products of trigonometric functions into equivalent expressions involving different trigonometric functions. These are particularly useful for solving trigonometric equations and simplifying expressions.
4. Hyperbolic Trigonometric Functions: These functions, often denoted as sinh x, cosh x, etc., are defined using exponential functions and share some similarities with trigonometric functions. They appear in various areas of physics and engineering.
Conclusion: The Importance of Clear Notation
While the expression "1 sin x 1 sin x" remains ambiguous without further context, exploring its potential interpretations has highlighted the fundamental importance of precise mathematical notation and the vast applications of trigonometric identities. Understanding the sine function and related identities is crucial in a wide array of scientific, engineering, and computational disciplines. Always strive for clarity and precision in your mathematical expressions to avoid confusion and ensure accurate results. The correct interpretation and manipulation of trigonometric expressions are paramount for success in numerous fields. Furthermore, mastering trigonometric concepts empowers you to solve complex problems, model real-world phenomena, and contribute meaningfully to various fields of study and industry.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 Sin X 1 Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.