10 Is 20 Percent Of What Number
News Co
May 07, 2025 · 5 min read
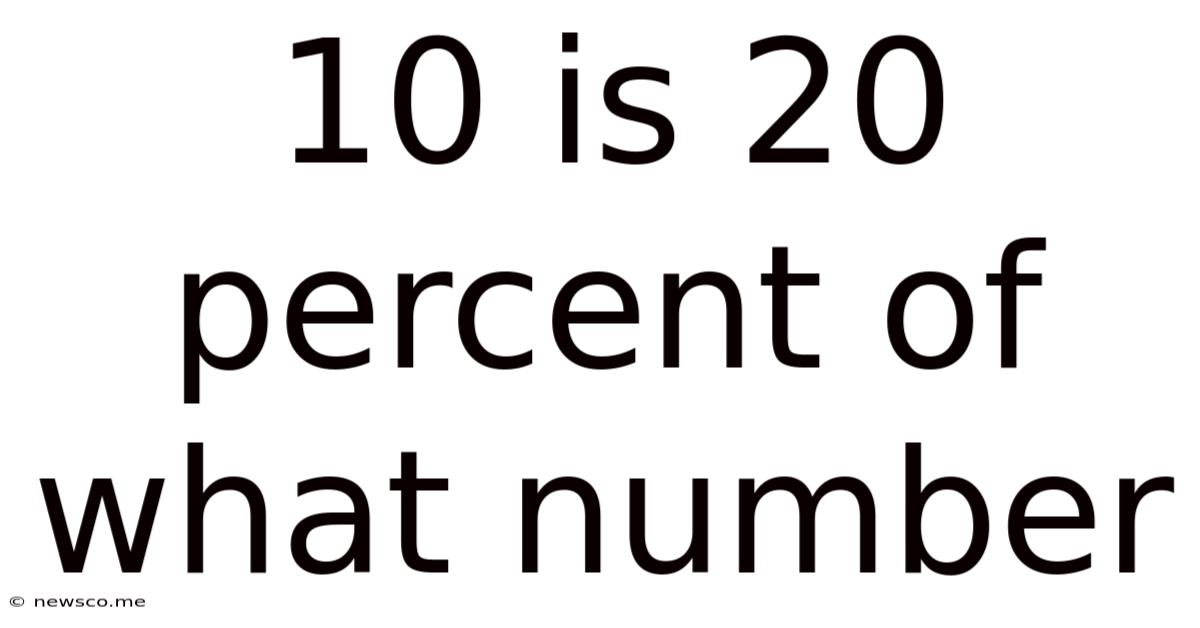
Table of Contents
- 10 Is 20 Percent Of What Number
- Table of Contents
- 10 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
- Understanding Percentages: The Foundation
- Method 1: The Algebraic Approach
- Method 2: The Proportion Method
- Method 3: The Formula Method
- Real-World Applications: Where Percentage Calculations Matter
- 1. Finance and Budgeting:
- 2. Business and Economics:
- 3. Science and Research:
- 4. Everyday Life:
- Tips for Mastering Percentage Calculations
- Beyond the Basics: More Complex Percentage Problems
- Conclusion: The Power of Percentage Calculations
- Latest Posts
- Related Post
10 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Finding out what number 10 represents 20% of is a fundamental percentage problem. While seemingly simple, understanding the underlying principles is crucial for tackling more complex percentage calculations in various fields, from finance and business to science and everyday life. This comprehensive guide will not only solve this specific problem but also equip you with the tools and strategies to confidently solve similar percentage questions. We’ll delve into different methods, explore real-world applications, and offer practical tips for mastering percentage calculations.
Understanding Percentages: The Foundation
Before tackling the problem at hand, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." Therefore, 20% can be written as 20/100, or its simplified fraction 1/5, or its decimal equivalent 0.2. This understanding forms the bedrock of all percentage calculations.
Method 1: The Algebraic Approach
This method uses algebra to solve the problem. We can represent the unknown number as 'x'. The problem can be expressed as an equation:
20% of x = 10
To solve for 'x', we translate the percentage into a decimal:
0.2x = 10
Now, we isolate 'x' by dividing both sides of the equation by 0.2:
x = 10 / 0.2
x = 50
Therefore, 10 is 20% of 50.
Method 2: The Proportion Method
This method uses proportions to solve the problem. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
20/100 = 10/x
This equation states that the ratio of 20 to 100 is equal to the ratio of 10 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
20x = 1000
Then, divide both sides by 20:
x = 1000 / 20
x = 50
Again, we find that 10 is 20% of 50.
Method 3: The Formula Method
A more direct formula can be derived from the algebraic method. If we want to find the whole number (let's call it 'W') when we know a percentage (P) of it is equal to a certain value (V), we can use the following formula:
W = V / (P/100)
In our case:
- V = 10
- P = 20
Substituting these values into the formula:
W = 10 / (20/100)
W = 10 / 0.2
W = 50
This confirms that 10 is 20% of 50.
Real-World Applications: Where Percentage Calculations Matter
Understanding percentage calculations is essential in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating discounts: Sales often advertise percentages off. Knowing how to calculate the actual discount amount allows consumers to make informed purchasing decisions. For example, a 25% discount on a $100 item means a savings of $25.
- Understanding interest rates: Interest on loans, savings accounts, and credit cards is expressed as a percentage. Calculating interest earned or owed is vital for managing personal finances.
- Analyzing investment returns: Investors use percentage calculations to track the performance of their investments and assess potential risks and rewards.
2. Business and Economics:
- Profit margins: Businesses calculate profit margins as a percentage of revenue to assess their profitability.
- Market share analysis: Companies use percentage calculations to analyze their market share and identify growth opportunities.
- Sales tax calculations: Businesses and consumers need to calculate sales tax, which is a percentage of the purchase price.
3. Science and Research:
- Data analysis: Percentages are frequently used to represent data in scientific research and studies. For instance, expressing the percentage of a population exhibiting a certain characteristic.
- Experimental results: Researchers often use percentages to express the success rate or effectiveness of experiments or treatments.
4. Everyday Life:
- Tipping in restaurants: Calculating a percentage tip is a common everyday application of percentage calculations.
- Calculating sales tax: Consumers often need to calculate sales tax on purchases.
- Understanding nutritional information: Nutritional labels often express the percentage of recommended daily intake of various nutrients.
Tips for Mastering Percentage Calculations
- Practice regularly: The key to mastering any mathematical concept is consistent practice. Solve various percentage problems to build your confidence and speed.
- Use different methods: Experiment with different methods (algebraic, proportion, formula) to find the approach that suits you best.
- Convert percentages to decimals or fractions: Converting percentages to decimals or fractions makes calculations easier and reduces the chances of errors.
- Check your work: Always double-check your answers to ensure accuracy.
- Use a calculator: For more complex calculations, using a calculator can save time and increase accuracy.
Beyond the Basics: More Complex Percentage Problems
While this article focuses on a fundamental percentage problem, the principles discussed can be applied to more complex scenarios. For instance, you might encounter problems involving percentage increase or decrease, compound interest, or percentage change over time. These involve similar fundamental principles but require additional steps and understanding.
Conclusion: The Power of Percentage Calculations
The ability to solve percentage problems, such as determining what number 10 is 20% of, is a valuable skill with wide-ranging applications. By understanding the underlying principles, practicing various methods, and applying the knowledge to real-world scenarios, you can master percentage calculations and confidently navigate situations where this skill is essential. Remember, consistent practice is the key to building fluency and accuracy. So, continue to practice, and you'll find yourself effortlessly solving percentage problems in no time! The ability to handle percentages confidently empowers you in numerous aspects of life, both personal and professional.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.