10 Is 30 Of What Number
News Co
May 07, 2025 · 4 min read
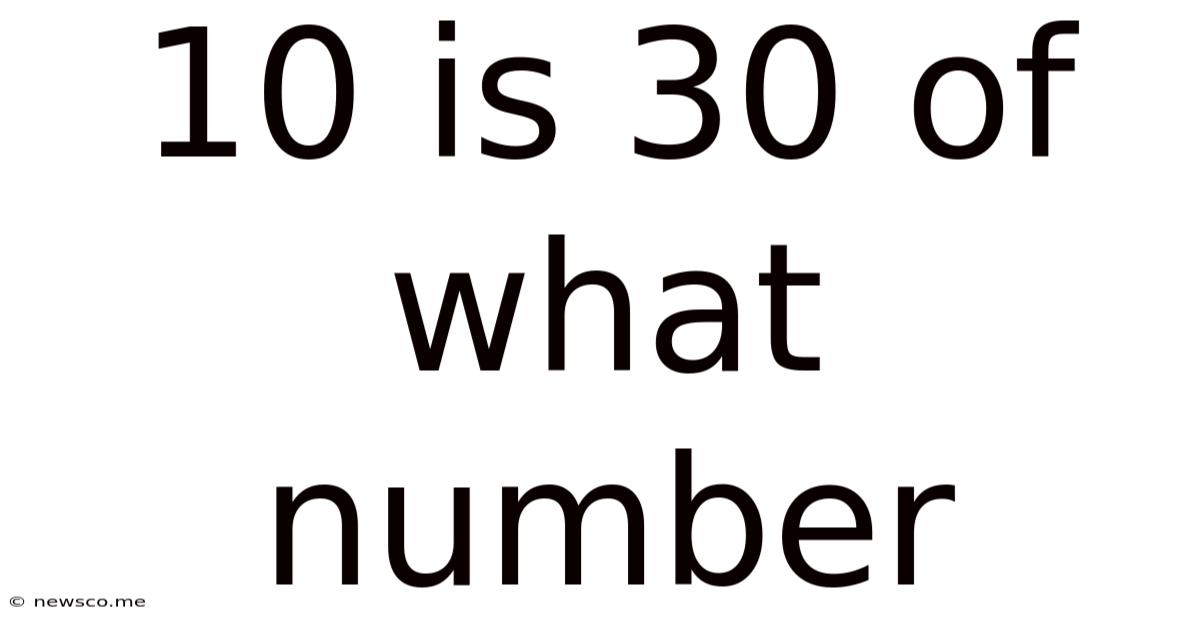
Table of Contents
10 is 30% of What Number? Unraveling the Math and its Applications
Finding a percentage of a number is a fundamental arithmetic operation with wide-ranging applications across various fields. This article will delve into the solution of the problem "10 is 30% of what number?", exploring not only the mathematical process but also its practical implications in everyday life, business, and beyond. We'll cover various methods of solving this type of problem, providing a comprehensive understanding for students and anyone seeking to improve their numerical skills.
Understanding Percentages and Proportions
Before diving into the solution, let's clarify the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For instance, 30% means 30 out of 100, which can also be represented as the fraction 30/100 or the decimal 0.3. The problem "10 is 30% of what number?" essentially asks us to find the whole number when we know a part of it (10) and the percentage that part represents (30%).
This problem can be elegantly solved using proportions. A proportion is a statement that equates two ratios. In this case, we can set up a proportion as follows:
10/x = 30/100
Where:
- 10 represents the part.
- x represents the unknown whole number we are trying to find.
- 30/100 represents the percentage (30%) expressed as a fraction.
Method 1: Solving the Proportion Directly
Solving the proportion above involves cross-multiplication. This involves multiplying the numerator of one fraction by the denominator of the other, and setting the two products equal to each other. This gives us:
10 * 100 = 30 * x
1000 = 30x
Now, to isolate 'x', we divide both sides of the equation by 30:
x = 1000/30
x = 33.333... (approximately)
Therefore, 10 is 30% of approximately 33.33.
Method 2: Using Decimal Equivalents
We can also solve this problem by converting the percentage to its decimal equivalent. As mentioned earlier, 30% is equal to 0.3. The problem can then be rewritten as:
10 = 0.3 * x
To solve for x, we divide both sides by 0.3:
x = 10 / 0.3
x = 33.333... (approximately)
This method provides the same result as the proportion method, confirming our answer.
Method 3: Working Backwards from the Percentage
Another approach is to consider the problem in reverse. If 30% of a number is 10, then 1% of that number would be 10 divided by 30:
1% = 10 / 30 = 0.333...
To find the whole number (100%), we simply multiply this value by 100:
100% = 0.333... * 100 = 33.333...
This method provides a clear and intuitive way to understand the relationship between the part, the percentage, and the whole.
Practical Applications: Where This Calculation Matters
The ability to calculate percentages and solve problems like "10 is 30% of what number?" has significant practical applications in many areas:
1. Business and Finance:
- Profit Margins: Businesses use percentage calculations to determine their profit margins. Knowing the profit and the percentage profit margin allows them to calculate the total revenue.
- Sales and Discounts: Sales and discounts are frequently expressed as percentages. Calculating the original price from a discounted price uses similar mathematical principles.
- Interest Rates: Understanding interest rates on loans and investments involves calculating percentages.
- Tax Calculations: Determining tax amounts payable requires calculating percentages of income or sales.
2. Everyday Life:
- Tips and Gratuities: Calculating tips in restaurants or other service industries involves finding a percentage of the total bill.
- Shopping: Comparing prices and evaluating discounts requires understanding percentages and their applications.
- Cooking and Baking: Many recipes provide ingredient amounts as percentages of the total weight or volume, requiring percentage calculations for scaling the recipe.
- Savings and Budgets: Tracking savings goals and managing household budgets often involves calculating percentages of income and expenses.
3. Science and Engineering:
- Data Analysis: Percentages are extensively used in statistical analysis and data representation.
- Chemistry and Physics: Concentration measurements in chemistry are often expressed as percentages, necessitating percentage calculations.
- Engineering Design: Many engineering calculations involve determining percentages of various components in a design or system.
4. Education and Academics:
- Grade Calculations: Calculating overall grades from individual assignments and tests involves weighting percentages.
- Statistical Analysis: Students across various disciplines utilize percentages in statistical analysis and data interpretation.
Expanding the Concept: Beyond Simple Percentages
The basic percentage calculation we've discussed can be expanded upon to handle more complex scenarios. These might include:
- Calculating multiple percentages: For example, determining the final price after successive discounts.
- Working with compound interest: Where interest is calculated not only on the principal but also on accumulated interest.
- Using percentages in more complex equations: This might involve incorporating percentages into more sophisticated mathematical formulas relevant to specific fields.
Conclusion: Mastering Percentage Calculations
The seemingly simple problem, "10 is 30% of what number?", reveals a fundamental mathematical concept with extensive real-world applications. Mastering this concept, along with various solution methods, equips individuals with valuable skills for everyday life, professional endeavors, and further mathematical explorations. Understanding how to manipulate percentages is crucial for informed decision-making across numerous fields, highlighting the importance of grasping this core mathematical principle. By practicing these methods and understanding their implications, you enhance your numerical literacy and problem-solving abilities significantly. Remember, the key is understanding the underlying principles, not just memorizing formulas. With practice and application, you'll become proficient in tackling percentage problems with ease and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Is 30 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.