10 Is What Percent Of 500
News Co
Apr 24, 2025 · 4 min read
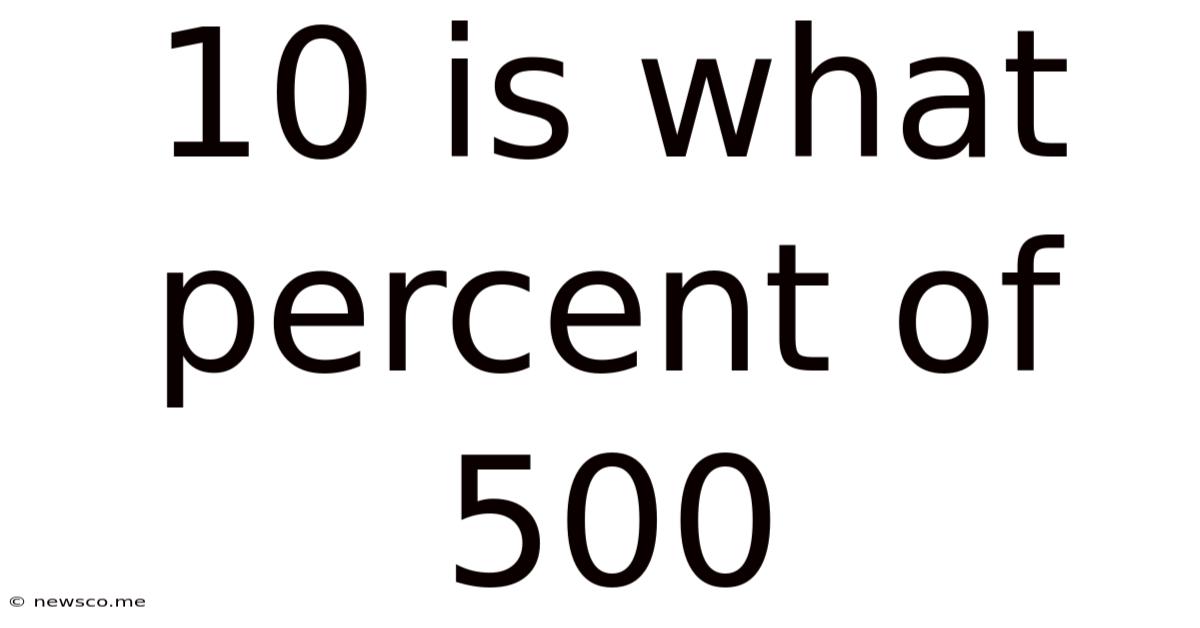
Table of Contents
10 is What Percent of 500? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article will thoroughly explore the question, "10 is what percent of 500?", providing not only the answer but also a comprehensive understanding of the underlying principles and various methods for solving percentage problems. We'll also delve into practical applications and related concepts to solidify your grasp of percentage calculations.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred," representing a portion of a whole. For instance, 50% signifies 50 out of 100, or one-half. Understanding this fundamental concept is crucial for tackling any percentage problem.
Calculating "10 is What Percent of 500?"
There are several approaches to solve this problem. Let's explore the most common and straightforward methods:
Method 1: Using the Formula
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 10
- Whole: 500
Substituting these values into the formula:
(10 / 500) * 100 = 2%
Therefore, 10 is 2% of 500.
Method 2: Proportion Method
This method uses proportions to solve percentage problems. We set up a proportion where:
- x/100 represents the unknown percentage
- 10/500 represents the given fraction
This creates the proportion:
x/100 = 10/500
To solve for 'x', we cross-multiply:
500x = 1000
Then divide both sides by 500:
x = 2
Therefore, x = 2%, confirming our previous result.
Method 3: Using Decimal Equivalents
We can convert the fraction 10/500 into a decimal by performing the division:
10 ÷ 500 = 0.02
To express this decimal as a percentage, multiply by 100:
0.02 * 100 = 2%
This method is particularly useful when working with calculators or spreadsheets.
Expanding on Percentage Concepts
Understanding the calculation of "10 is what percent of 500?" is just the first step. Let's explore related concepts that build upon this foundational knowledge:
Finding the Whole When Given the Percentage and Part
Often, you might need to determine the whole amount when you know a percentage and its corresponding part. For instance: "2% of what number is 10?"
The formula here is adapted to:
(Part / Percentage) * 100 = Whole
(10 / 2) * 100 = 500
This demonstrates the reverse calculation, confirming that 10 is indeed 2% of 500.
Finding the Part When Given the Percentage and Whole
Alternatively, you might need to find the part when given the percentage and the whole. For example: "What is 2% of 500?"
The formula remains:
(Percentage / 100) * Whole = Part
(2 / 100) * 500 = 10
This calculation reinforces our initial findings.
Percentage Increase and Decrease
Percentages are frequently used to describe increases or decreases in values. For instance, if a price increases by 10%, we calculate the increase and add it to the original price. Similarly, a 10% decrease is calculated and subtracted from the original price. Understanding these applications is vital for analyzing trends and changes in various contexts.
Applications of Percentage Calculations in Real Life
The applications of percentage calculations are vast and span numerous areas of life:
- Finance: Calculating interest rates, discounts, profits, losses, taxes, and investment returns all involve percentages.
- Retail: Determining sale prices, discounts, and markups relies heavily on percentage calculations.
- Science: Representing data, analyzing experimental results, and expressing concentrations often involve percentages.
- Statistics: Percentages are used to present data concisely and for statistical analysis.
- Everyday Life: Calculating tips, figuring out sale prices, and understanding tax rates are all common applications of percentages.
Advanced Percentage Problems & Strategies
While the problem "10 is what percent of 500?" is relatively straightforward, more complex percentage problems may require multi-step calculations or the use of algebraic equations. These might involve scenarios with multiple percentage changes, compound interest, or problems requiring simultaneous equation solving. For these more complex scenarios, a strong foundation in algebraic principles is helpful. Practicing a range of problems, from simple to complex, will solidify your understanding and build your confidence in tackling various percentage-based challenges.
Tips for Mastering Percentage Calculations
- Practice regularly: Consistent practice is key to mastering any mathematical concept, including percentages. Work through various examples and problem types to solidify your understanding.
- Use multiple methods: Try different approaches (formula, proportion, decimal equivalents) to reinforce your learning and identify the method that works best for you.
- Understand the context: Pay close attention to the problem's wording to correctly identify the part, whole, and percentage.
- Check your work: Always double-check your calculations to ensure accuracy.
- Utilize online resources: Numerous online resources, including calculators and tutorials, can provide additional assistance and practice opportunities.
Conclusion: Beyond the Numbers
This comprehensive exploration of "10 is what percent of 500?" extends beyond the simple calculation of 2%. It highlights the fundamental principles of percentages, their widespread applications, and provides strategies for tackling more complex problems. Mastering percentage calculations empowers you to analyze data, make informed decisions, and confidently navigate various aspects of life, from personal finance to professional endeavors. Remember, consistent practice and a thorough understanding of the underlying concepts are crucial for success. So, keep practicing, and you’ll soon become a percentage pro!
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.