10 Of What Number Is 30
News Co
May 07, 2025 · 4 min read
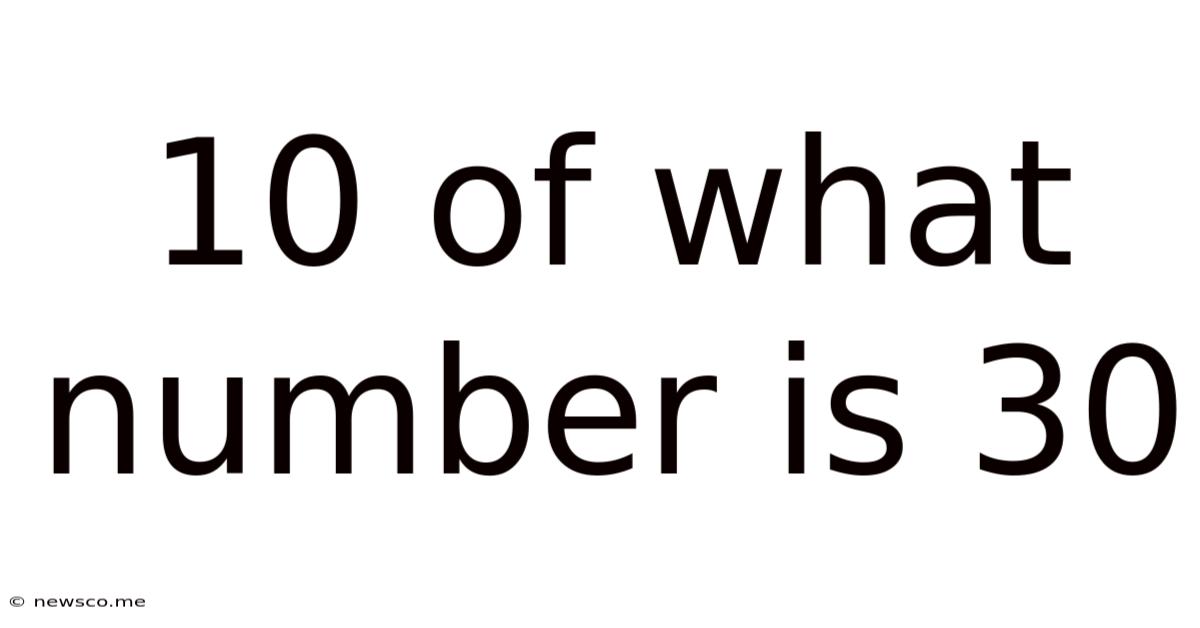
Table of Contents
10 of What Number is 30? Unpacking a Simple Equation and its Broader Mathematical Implications
The seemingly simple question, "10 of what number is 30?" is a gateway to understanding fundamental mathematical concepts. While the answer itself is straightforward, exploring the question allows us to delve into the world of algebra, ratios, proportions, and even real-world applications. This article will not only provide the solution but also unpack the underlying principles, offering a comprehensive exploration for both beginners and those seeking a refresher.
Understanding the Problem: Deconstructing the Question
The phrase "10 of what number is 30" can be easily translated into a mathematical equation. Let's break it down:
- "10 of" signifies multiplication. We are dealing with a multiplication problem.
- "what number" represents the unknown variable, which we can symbolize with 'x' (or any other letter).
- "is 30" indicates equality. The result of the multiplication equals 30.
Therefore, the equation becomes: 10 * x = 30
Solving the Equation: Finding the Unknown
Solving for 'x' involves isolating the variable. In this case, we need to undo the multiplication operation. This is achieved by performing the inverse operation – division. We divide both sides of the equation by 10:
10 * x / 10 = 30 / 10
This simplifies to:
x = 3
Therefore, the answer to the question, "10 of what number is 30?" is 3.
Beyond the Answer: Exploring Related Concepts
While finding the answer is crucial, understanding the broader mathematical context significantly enhances comprehension. Let's explore related concepts illuminated by this simple equation:
1. Ratios and Proportions
The equation 10 * x = 30 can be viewed as a ratio or proportion. We can express this as:
10 : x = 30 : 3 (This reads as "10 is to x as 30 is to 3")
This proportion demonstrates the relationship between two sets of numbers. Understanding ratios and proportions is vital in various fields, including scaling recipes, calculating map distances, and analyzing financial data.
2. Algebraic Thinking: The Power of Variables
The use of 'x' to represent the unknown number introduces the fundamental concept of variables in algebra. Variables allow us to represent unknown quantities, enabling us to solve for them using algebraic manipulations. This ability to represent unknowns is essential for tackling complex mathematical problems.
3. Inverse Operations: Undoing Mathematical Actions
Solving the equation required using the inverse operation of multiplication (division). Understanding inverse operations – like addition and subtraction, or multiplication and division – is crucial for manipulating equations and solving for unknown variables.
4. Real-World Applications: Where this Equation Might Appear
This seemingly simple equation has numerous real-world applications. Consider these scenarios:
- Division of Goods: If you have 30 apples to divide equally among 10 people, each person receives 3 apples (30 / 10 = 3).
- Pricing: If 10 items cost $30, then one item costs $3 ($30 / 10 = $3).
- Measurement Conversion: Converting units often involves similar calculations. For example, if 10 centimeters equal 30 millimeters, then one centimeter equals 3 millimeters.
Extending the Learning: Similar Problems and Advanced Concepts
Once you've grasped the fundamentals, let's explore more complex variations of this type of problem:
1. Solving for Different Variables
Instead of solving for the number multiplied by 10, we could alter the problem. For example:
- What number multiplied by 3 is equal to 30? (This translates to 3x = 30, solving for x = 10)
- 10 multiplied by what number is 150? (This translates to 10x = 150, solving for x = 15)
These variations reinforce the understanding of how to manipulate equations to solve for different unknowns.
2. Introducing Fractions and Decimals
Let's introduce fractions and decimals into the equation:
- 10 of what number is 15? (This translates to 10x = 15, solving for x = 1.5)
- 10 of what number is 25/5? (First simplify the fraction: 25/5 = 5. Then the equation becomes 10x = 5, solving for x = 0.5)
These examples demonstrate that the principle remains the same even with different numerical forms.
3. Word Problems and Real-World Applications
Applying these mathematical concepts to word problems is essential for developing problem-solving skills. For instance:
- "A baker uses 10 cups of flour to make 30 muffins. How many cups of flour are needed per muffin?"
- "A car travels 30 kilometers in 10 minutes. What is its speed in kilometers per minute?"
These scenarios require translating the word problem into a mathematical equation, then applying the appropriate techniques to find the solution.
Conclusion: The Importance of Building a Strong Foundation
The simple equation 10 * x = 30, while seemingly basic, offers a profound glimpse into the fundamental concepts of mathematics. From understanding ratios and proportions to mastering algebraic manipulations and applying these skills to real-world scenarios, this equation provides a springboard for further learning. The ability to solve this type of problem, and others like it, is not only crucial for academic success but also essential for navigating many aspects of everyday life. By consistently practicing and exploring these concepts, you will build a solid mathematical foundation that will serve you well in your academic pursuits and beyond. Remember that mathematical literacy is a valuable skill, and mastering even the simplest equations contributes to your overall intellectual growth.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Of What Number Is 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.