10 To The 5th Power Equals
News Co
Apr 25, 2025 · 5 min read
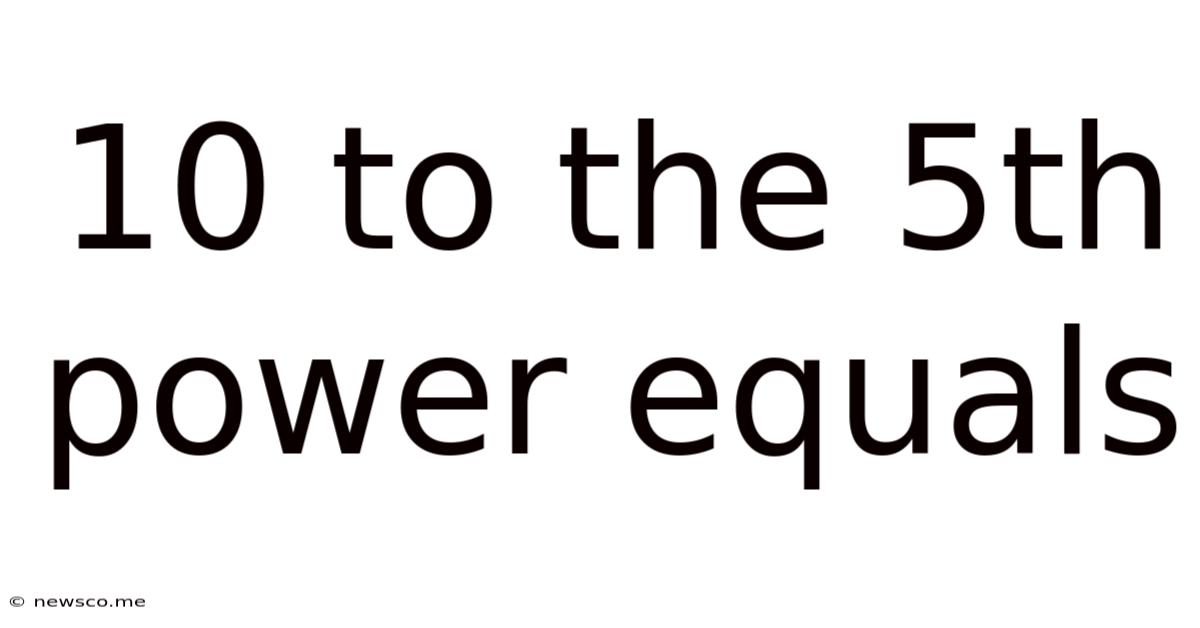
Table of Contents
10 to the 5th Power Equals: Unpacking Exponential Notation and its Applications
Understanding exponential notation, like 10 to the 5th power, is fundamental to grasping many areas of mathematics, science, and even everyday life. This seemingly simple calculation – 10⁵ – opens the door to comprehending larger numbers, scientific measurements, and the power of exponential growth. This article will delve deep into the meaning of 10⁵, explore its applications, and demonstrate its relevance across various disciplines.
What Does 10 to the 5th Power Mean?
At its core, 10⁵ means 10 multiplied by itself five times: 10 x 10 x 10 x 10 x 10. This process of repeated multiplication is the essence of exponentiation. The number 10 is called the base, and the number 5 is called the exponent or power. The exponent tells us how many times the base is multiplied by itself.
Therefore, 10⁵ = 100,000 (one hundred thousand).
This simple calculation might seem insignificant at first glance, but its implications are far-reaching. Let's explore why.
Understanding Exponential Growth
The concept of 10⁵ illustrates exponential growth. Exponential growth isn't just about a large number; it's about a rate of growth where the increase is proportional to the current value. Imagine a population of bacteria doubling every hour. This is exponential growth. In contrast, linear growth would involve a constant increase, like adding a fixed number of bacteria each hour. Exponential growth accelerates rapidly, becoming vastly larger than linear growth over time.
Examples of Exponential Growth:
- Compound Interest: The interest you earn on your savings account is often compounded, meaning interest is calculated on the principal plus accumulated interest. This compounding effect leads to exponential growth of your savings over time.
- Viral Marketing: The spread of information or ideas through social media networks often follows an exponential pattern. A single post can be shared with many people, who then share it with even more, leading to a rapid increase in reach.
- Population Growth: Under ideal conditions, population growth can follow an exponential pattern, with each generation producing more offspring than the previous one. This can lead to rapid increases in population size.
Scientific Notation and 10 to the 5th Power
Scientific notation is a powerful tool used to represent very large or very small numbers concisely. It utilizes powers of 10 to express these numbers. For instance, the speed of light is approximately 3 x 10⁸ meters per second. This is much more manageable than writing out 300,000,000. Similarly, the mass of an electron is approximately 9.1 x 10⁻³¹ kilograms. 10⁵, therefore, plays a crucial role in understanding the scale of numbers in scientific contexts.
Using 10⁵ in Scientific Calculations:
Consider a scenario involving the calculation of the volume of a cube with sides measuring 100 meters each. The volume is calculated as 100 x 100 x 100 = 1,000,000 cubic meters. Using scientific notation, this can be expressed as 1 x 10⁶ cubic meters. Observe the relationship between 10⁵ and 10⁶, highlighting the importance of understanding powers of 10 in handling large quantities.
10 to the 5th Power in Measurement Units
The metric system relies heavily on powers of 10 for its unit prefixes. Understanding 10⁵ helps us readily convert between units. For example:
- Kilometers: One kilometer (km) equals 1000 meters (m), or 10³ m.
- Megabytes: One megabyte (MB) equals 1,048,576 bytes, often approximated to 10⁶ bytes. While not exactly 10⁵, understanding the exponential relationship allows for quick estimations.
Therefore, familiarity with 10⁵ provides a strong base for grasping larger units and easier conversions within the metric system.
Beyond 10⁵: Exploring Higher Powers of 10
Understanding 10⁵ serves as a springboard to understanding higher powers of 10. This includes:
- 10⁶ (one million): Represents a significantly larger quantity, often used to represent large populations, financial amounts, or data sizes.
- 10⁹ (one billion): Used to describe national budgets, global populations, or astronomical distances.
- 10¹² (one trillion): Used in describing national debts, global economies, or the number of atoms in a small amount of matter.
Mastering 10⁵ is the crucial first step in comfortably working with these larger numbers and comprehending their scale.
Practical Applications of 10⁵
The application of 10⁵ extends far beyond theoretical mathematics. Consider these examples:
- Data Storage: Many hard drives and storage devices have capacities measured in megabytes (MB), gigabytes (GB), or terabytes (TB), all of which are powers of 10. Understanding 10⁵ helps us estimate storage needs and compare different storage options.
- Finance: Financial calculations frequently involve large numbers, making a grasp of exponential notation critical. Calculating compound interest, analyzing investment returns, or evaluating loan repayments all require an understanding of exponential growth.
- Engineering: Engineers often deal with large structures or complex systems. Understanding large numbers and exponential notation is crucial for scaling designs, estimating material requirements, and analyzing system performance.
- Computer Science: Binary code and digital systems rely heavily on powers of 2. While not directly 10⁵, the principle of exponential notation remains fundamental to understanding how these systems function.
Addressing Common Misconceptions
One common mistake is confusing 10⁵ with 5 x 10 or 10 + 10 + 10 + 10 + 10. Remember, the exponent dictates repeated multiplication, not addition or simple multiplication of the base and exponent.
Another misconception revolves around the apparent "smallness" of the base (10). While 10 might seem a relatively small number, its repeated multiplication through exponentiation leads to an incredibly rapid increase in value, highlighting the power of exponential growth.
Conclusion: The Significance of 10⁵
10 to the 5th power, equaling 100,000, might initially appear as a straightforward calculation. However, a deeper exploration reveals its immense significance across various fields. From understanding exponential growth and scientific notation to applying it in practical scenarios involving data storage, finance, and engineering, 10⁵ plays a vital role in our comprehension of the world around us. Mastering this fundamental concept unlocks a gateway to handling larger numbers, comprehending scientific concepts, and solving real-world problems. Its importance in scientific notation and metric system conversions cannot be overstated. Understanding 10⁵ is not just about knowing the answer; it's about grasping the power of exponential notation and its wide-ranging applications. Therefore, cementing this understanding is crucial for success in numerous academic and professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 To The 5th Power Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.