12.5 Percent As A Fraction In Simplest Form
News Co
May 08, 2025 · 4 min read
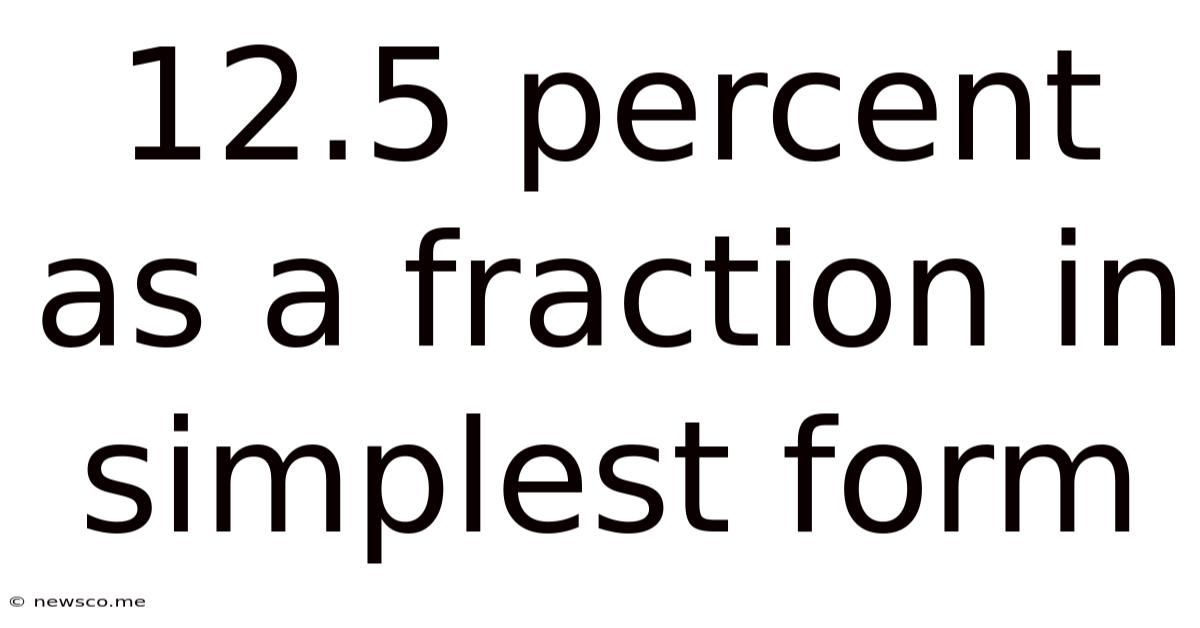
Table of Contents
12.5 Percent as a Fraction in Simplest Form: A Comprehensive Guide
Understanding percentages, decimals, and fractions is fundamental in mathematics and numerous real-world applications. Converting between these forms is a crucial skill, and this article delves deep into the process of expressing 12.5 percent as a fraction in its simplest form. We’ll not only show you the solution but also explore the underlying concepts and offer practical examples to solidify your understanding. This comprehensive guide aims to provide a thorough grasp of percentage-fraction conversion, beneficial for students, professionals, and anyone seeking to improve their mathematical skills.
Understanding Percentages and Fractions
Before we tackle the conversion of 12.5 percent, let's review the fundamental definitions:
-
Percentage: A percentage represents a fraction of 100. The word "percent" literally means "per hundred." Therefore, 12.5 percent means 12.5 out of 100.
-
Fraction: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, ½ represents one part out of two equal parts.
-
Decimal: A decimal is a number expressed in the base-10 numeral system, using a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half.
Converting 12.5 Percent to a Fraction
The conversion process involves several straightforward steps:
Step 1: Write the Percentage as a Fraction with a Denominator of 100
Since percentage means "per hundred," we can write 12.5 percent as the fraction:
12.5/100
Step 2: Eliminate the Decimal Point
Decimal numbers in fractions are generally less desirable. To remove the decimal point in the numerator, we can multiply both the numerator and the denominator by 10 (since there's one digit after the decimal point):
(12.5 * 10) / (100 * 10) = 125/1000
Step 3: Simplify the Fraction
Now, we need to simplify the fraction to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 125 and 1000 is 125. Therefore:
125/1000 = (125 ÷ 125) / (1000 ÷ 125) = 1/8
Therefore, 12.5 percent expressed as a fraction in its simplest form is 1/8.
Alternative Method: Converting to Decimal First
An alternative approach involves converting the percentage to a decimal first, then converting the decimal to a fraction.
Step 1: Convert Percentage to Decimal
To convert a percentage to a decimal, divide the percentage by 100:
12.5% ÷ 100 = 0.125
Step 2: Convert Decimal to Fraction
The decimal 0.125 can be written as a fraction:
0.125 = 125/1000
Step 3: Simplify the Fraction
As before, we simplify the fraction by finding the GCD (125) and dividing both the numerator and denominator by it:
125/1000 = 1/8
Again, we arrive at the simplest form: 1/8
Practical Applications of Percentage to Fraction Conversion
The ability to convert percentages to fractions is crucial in many areas:
-
Finance: Calculating interest rates, discounts, and profit margins often requires converting percentages to fractions. For example, a 12.5% discount on a $100 item means a discount of (1/8) * $100 = $12.50.
-
Cooking and Baking: Recipes sometimes specify ingredients as percentages of the total weight or volume. Converting these percentages to fractions simplifies the measurement process.
-
Data Analysis and Statistics: Percentages are frequently used to represent data proportions. Converting them to fractions allows for easier comparison and calculations.
-
Geometry and Measurement: Calculations involving areas, volumes, and proportions often necessitate converting percentages to fractions for accurate results.
-
Everyday Life: Numerous everyday situations require understanding and converting percentages to fractions. For instance, calculating tips, determining sale prices, or understanding proportions in various contexts.
Further Exploration: Working with More Complex Percentages
The process outlined above can be applied to converting any percentage into a fraction. Let’s look at a few examples:
- 25%: 25/100 = 1/4
- 50%: 50/100 = 1/2
- 75%: 75/100 = 3/4
- 37.5%: 37.5/100 = 375/1000 = 3/8
- 62.5%: 62.5/100 = 625/1000 = 5/8
The key is to understand the fundamental principles: write the percentage as a fraction over 100, eliminate any decimal points by multiplying appropriately, and then simplify the resulting fraction to its lowest terms by finding the greatest common divisor of the numerator and denominator.
Tips for Simplifying Fractions
Simplifying fractions efficiently is key to mastering this conversion process. Here are some helpful strategies:
-
Prime Factorization: Break down both the numerator and denominator into their prime factors. This helps identify the GCD more easily.
-
Division by Common Factors: Systematically divide both the numerator and the denominator by common factors until you arrive at a fraction where no further division is possible.
-
Using a GCD Calculator: For larger numbers, a GCD calculator can be a useful tool to quickly determine the greatest common divisor.
Mastering fraction simplification ensures accuracy and efficiency in all your percentage-to-fraction conversions.
Conclusion
Converting 12.5 percent to its simplest fraction form, 1/8, is a straightforward process that relies on a clear understanding of percentages, fractions, and decimal numbers. This detailed guide has demonstrated two methods for achieving this conversion, along with practical applications and tips for simplifying fractions. By understanding these concepts and practicing the conversion steps, you will enhance your mathematical proficiency and confidently tackle similar problems in various contexts. Remember, consistent practice is key to mastering these essential mathematical skills.
Latest Posts
Latest Posts
-
The Product Of 7 And A Number Squared Is 28
May 08, 2025
-
A Rectangle With Four Equal Sides
May 08, 2025
-
Find The Area Of A Triangle Abc
May 08, 2025
-
Which Statement Is True About The Angles In Triangle Pqr
May 08, 2025
-
16 As A Fraction Of An Inch
May 08, 2025
Related Post
Thank you for visiting our website which covers about 12.5 Percent As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.