12 7 As A Mixed Number
News Co
Apr 08, 2025 · 5 min read
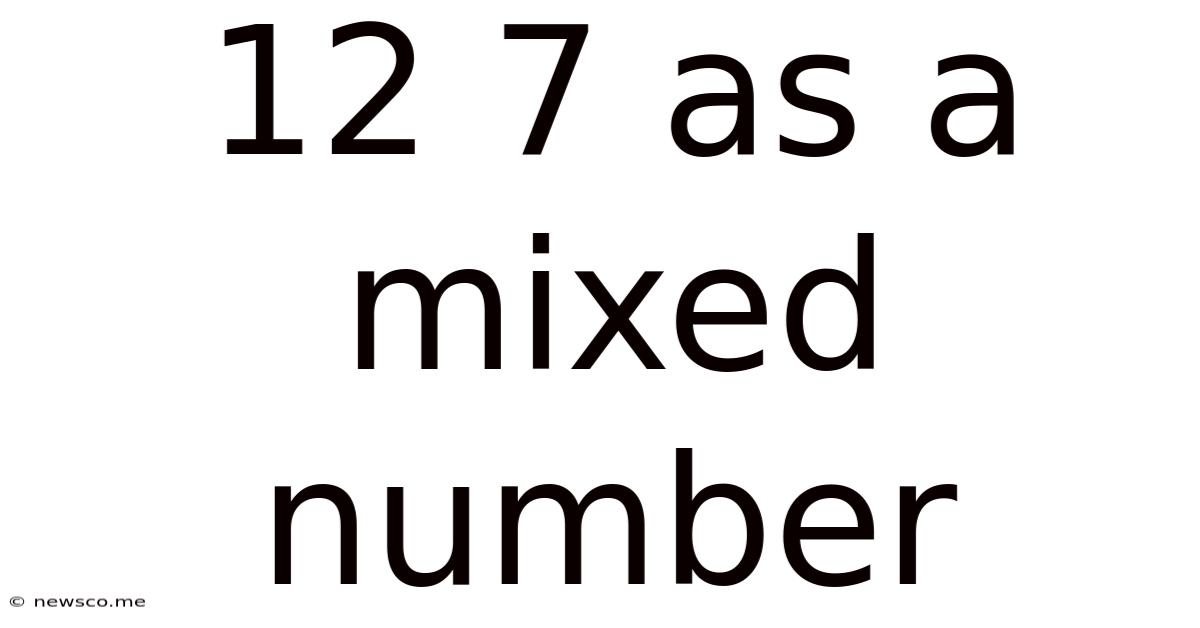
Table of Contents
12/7 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversion to mixed numbers is a fundamental concept in mathematics. This comprehensive guide delves deep into the process of converting the improper fraction 12/7 into a mixed number, exploring the underlying principles and providing practical examples. We’ll also discuss why this conversion is useful and explore related concepts.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion of 12/7, let's clarify the definitions:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 12/7 is an improper fraction because 12 (numerator) is greater than 7 (denominator).
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than its denominator. For instance, 1 ¾ is a mixed number.
Converting an improper fraction to a mixed number essentially represents the fraction in a more readily understandable format. It shows how many whole units are contained within the fraction and the remaining fractional part.
Converting 12/7 to a Mixed Number: Step-by-Step Guide
The conversion of 12/7 to a mixed number involves dividing the numerator by the denominator. Here’s how:
Step 1: Divide the numerator by the denominator.
12 ÷ 7 = 1 with a remainder of 5
Step 2: The quotient becomes the whole number part of the mixed number.
The quotient, 1, becomes the whole number part of our mixed number.
Step 3: The remainder becomes the numerator of the fractional part.
The remainder, 5, becomes the numerator of the fraction in our mixed number.
Step 4: The denominator remains the same.
The denominator remains 7.
Step 5: Combine the whole number and the fraction.
Therefore, 12/7 as a mixed number is 1 ⁵⁄₇.
Visual Representation of 12/7
Imagine you have 12 pizzas, and you want to share them equally among 7 friends. Each friend would receive one whole pizza (that’s our whole number 1). You would then have 5 pizzas left over, which need to be shared among the 7 friends. This leftover portion is represented by the fraction ⁵⁄₇. So, each friend gets 1 ⁵⁄₇ pizzas.
Why Convert Improper Fractions to Mixed Numbers?
Converting improper fractions to mixed numbers offers several advantages:
-
Improved Understanding: Mixed numbers are generally easier to understand and visualize than improper fractions. It’s simpler to grasp the concept of “1 and ⁵⁄₇ pizzas” than “12/7 pizzas.”
-
Easier Comparisons: Comparing mixed numbers is often easier than comparing improper fractions. For instance, comparing 1 ⁵⁄₇ to 2 is straightforward; you immediately see that 1 ⁵⁄₇ is less than 2.
-
Real-world Applications: Many real-world situations naturally lend themselves to mixed numbers. Measurements, quantities, and proportions often involve whole units and fractions of a unit.
-
Simplified Calculations: In some calculations, using mixed numbers can simplify the process. For instance, adding mixed numbers is often more intuitive than adding improper fractions.
Practice Problems: Converting Improper Fractions to Mixed Numbers
Let's practice converting more improper fractions to mixed numbers to solidify our understanding:
-
17/5: Dividing 17 by 5 gives a quotient of 3 and a remainder of 2. Therefore, 17/5 = 3 ²⁄₅.
-
22/3: Dividing 22 by 3 gives a quotient of 7 and a remainder of 1. Therefore, 22/3 = 7 ¹⁄₃.
-
31/8: Dividing 31 by 8 gives a quotient of 3 and a remainder of 7. Therefore, 31/8 = 3 ⁷⁄₈.
-
25/4: Dividing 25 by 4 gives a quotient of 6 and a remainder of 1. Therefore, 25/4 = 6 ¹⁄₄.
-
40/9: Dividing 40 by 9 gives a quotient of 4 and a remainder of 4. Therefore, 40/9 = 4 ⁴⁄₉.
Converting Mixed Numbers Back to Improper Fractions
It's also crucial to understand the reverse process: converting mixed numbers back to improper fractions. This involves the following steps:
-
Multiply the whole number by the denominator.
-
Add the product to the numerator.
-
Keep the same denominator.
Let's convert 1 ⁵⁄₇ back to an improper fraction:
-
1 (whole number) × 7 (denominator) = 7
-
7 + 5 (numerator) = 12
-
The denominator remains 7.
Therefore, 1 ⁵⁄₇ = 12/7.
Applications of Improper Fractions and Mixed Numbers
Improper fractions and mixed numbers have numerous applications across various fields:
-
Cooking and Baking: Recipes often use fractions and mixed numbers to specify ingredient quantities.
-
Construction and Engineering: Precise measurements in construction and engineering rely heavily on fractions and mixed numbers.
-
Sewing and Tailoring: Pattern cutting and garment construction involve careful measurements using fractions and mixed numbers.
-
Data Analysis: Fractions and mixed numbers often appear in data analysis and statistical calculations.
Beyond the Basics: Working with Mixed Numbers
Beyond simple conversion, you'll encounter more complex operations with mixed numbers, including:
-
Adding and Subtracting Mixed Numbers: This often involves converting to improper fractions first for easier calculation, and then converting the result back to a mixed number.
-
Multiplying and Dividing Mixed Numbers: Similar to addition and subtraction, converting to improper fractions often simplifies these operations.
-
Comparing Mixed Numbers: Direct comparison is often easiest, though converting to decimals can also aid in comparing mixed numbers.
Mastering the conversion of improper fractions to mixed numbers and vice versa is a crucial building block for advanced mathematical concepts. Practice consistently, and you'll build a strong foundation in fraction manipulation. Remember to visualize the concepts to enhance understanding and improve your problem-solving abilities. This comprehensive guide should equip you with the tools to confidently handle improper fractions and mixed numbers in various mathematical contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.