12 Divided By 5 As A Fraction
News Co
Mar 22, 2025 · 5 min read
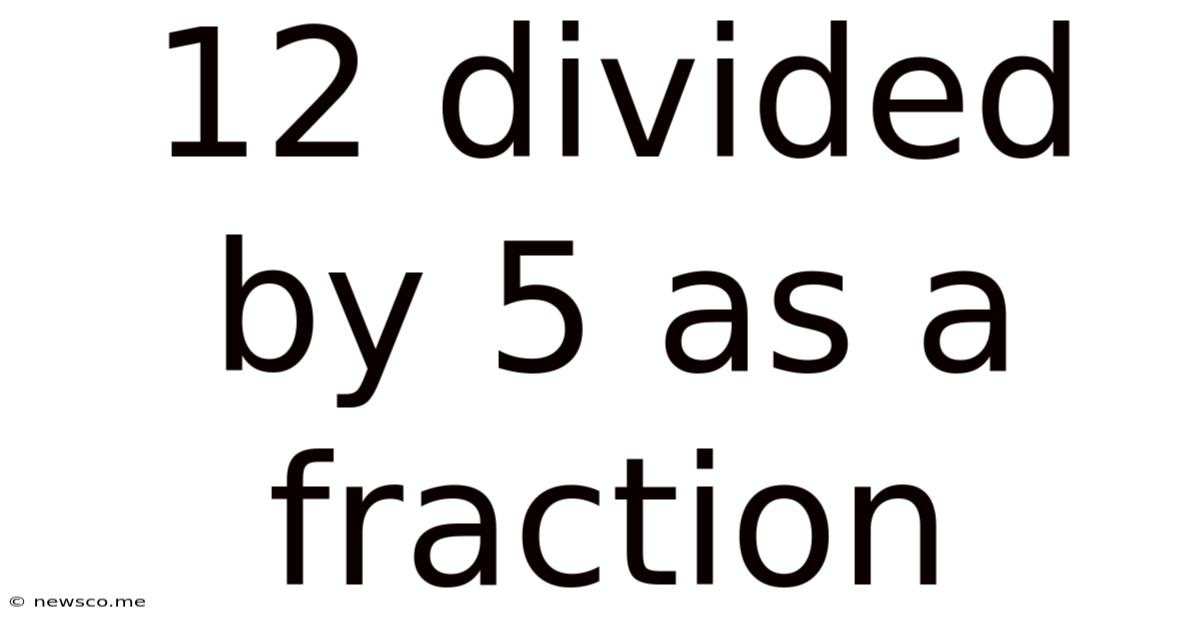
Table of Contents
12 Divided by 5 as a Fraction: A Comprehensive Guide
Dividing numbers can seem straightforward, but understanding the nuances, especially when representing the result as a fraction, can significantly enhance your mathematical abilities. This comprehensive guide delves into the process of dividing 12 by 5 and expressing the answer as a fraction, covering various aspects and related concepts. We will explore the problem from different angles, reinforcing the understanding of fractions and division.
Understanding the Basics: Division and Fractions
Before diving into the specific problem of 12 divided by 5, let's solidify our understanding of the core concepts: division and fractions.
What is Division?
Division is the process of splitting a quantity into equal parts or groups. It's the inverse operation of multiplication. When we say "12 divided by 5," we're asking how many times 5 goes into 12, or what is the size of each part when 12 is split into 5 equal parts.
What is a Fraction?
A fraction represents a part of a whole. It has two parts: a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction ¾, the numerator (3) represents three parts, and the denominator (4) means the whole is divided into four equal parts.
Calculating 12 Divided by 5 as a Fraction
Now, let's tackle the problem: 12 divided by 5.
Step 1: Perform the Division
We can perform the division using long division:
2
5 | 12
10
2
This shows that 5 goes into 12 two times with a remainder of 2.
Step 2: Expressing the Result as a Mixed Number
The result of 2 with a remainder of 2 can be written as a mixed number. A mixed number combines a whole number and a fraction. In this case, it's 2 and 2/5. This means we have two whole groups of 5, and a remainder of 2 parts out of a total of 5 parts needed to make another whole group. So, 12 divided by 5 equals 2 2/5.
Step 3: Expressing the Result as an Improper Fraction
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. To convert the mixed number 2 2/5 to an improper fraction, we follow these steps:
- Multiply the whole number (2) by the denominator (5): 2 * 5 = 10
- Add the numerator (2) to the result: 10 + 2 = 12
- Keep the same denominator (5): 12/5
Therefore, 12 divided by 5 expressed as an improper fraction is 12/5.
Deep Dive into Fractions: Equivalent Fractions, Simplification, and More
Understanding fractions goes beyond simple calculations. Let's explore some important related concepts.
Equivalent Fractions
Equivalent fractions represent the same value, even though they look different. For instance, ½, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half. We can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number (other than zero).
Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their GCD, which is 6. This simplifies to 2/3.
In the case of 12/5, the fraction is already in its simplest form because the GCD of 12 and 5 is 1.
Comparing Fractions
Comparing fractions involves determining which fraction is larger or smaller. This can be done by finding a common denominator or by converting the fractions to decimals.
Practical Applications of 12 Divided by 5
Understanding how to divide 12 by 5 and represent it as a fraction has many practical applications in various areas:
-
Baking and Cooking: Dividing ingredients for recipes often involves fractions. If a recipe calls for 12 ounces of flour and you want to make 5/5 (the whole recipe) you'd need to know how much flour goes into each portion.
-
Measurement and Construction: Measuring lengths, areas, and volumes often involves fractions and decimals. Construction work requires precise measurements, and understanding fractions is vital for accurate calculations.
-
Finance and Budgeting: Dividing budgets and calculating portions of expenses frequently requires working with fractions.
-
Data Analysis and Statistics: Representing data and calculating proportions often involves fractions.
Advanced Concepts: Decimal Representation and Percentage
While we've focused on fractions, it's useful to understand how the result of 12 divided by 5 can be represented in other forms.
Decimal Representation
To convert the fraction 12/5 to a decimal, we perform the division: 12 ÷ 5 = 2.4. This decimal representation offers another way to express the result of the division.
Percentage Representation
To convert the decimal 2.4 to a percentage, we multiply by 100: 2.4 * 100 = 240%. This indicates that 12 is 240% of 5.
Conclusion: Mastering Fractions and Division
Mastering division and the representation of results as fractions is a fundamental skill in mathematics. Understanding the concepts of equivalent fractions, simplification, and the different ways to represent a result (mixed number, improper fraction, decimal, percentage) allows for a more versatile and effective approach to problem-solving in various fields. The seemingly simple problem of 12 divided by 5 provides a solid foundation for understanding these broader mathematical concepts. Remember to practice regularly to improve your skills and confidence in working with fractions and division. Through consistent practice and application, you will find that these concepts become intuitive and easy to use. Further exploration into more complex division problems and fraction manipulation will only build upon this foundation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 Divided By 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.