12 Is 15 Percent Of What
News Co
Mar 16, 2025 · 5 min read
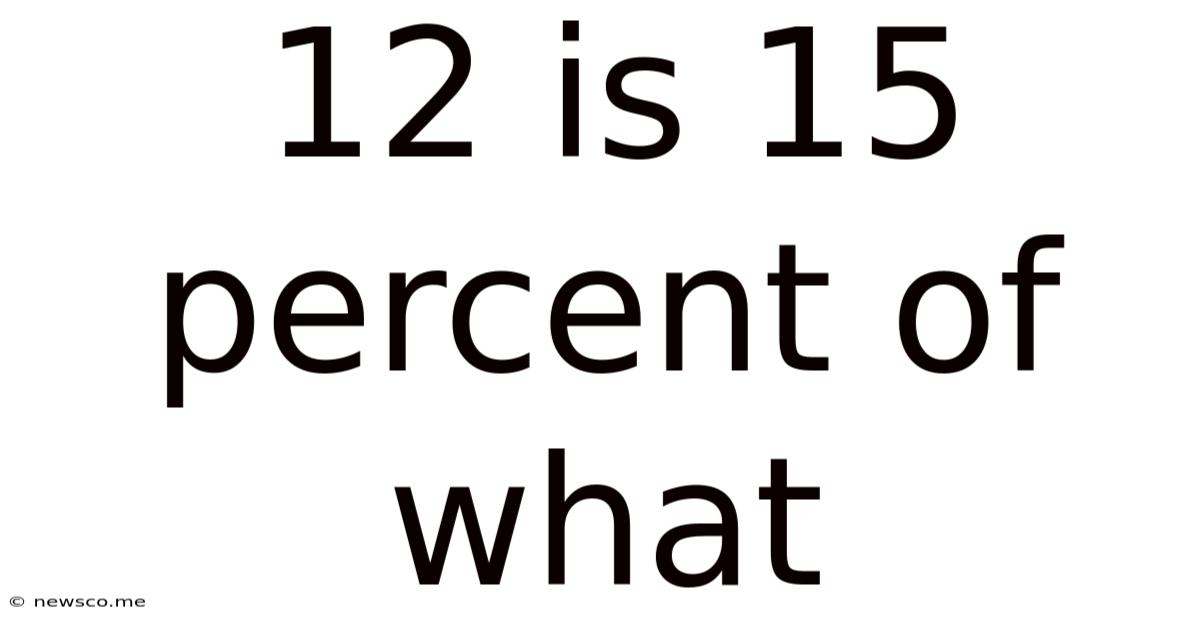
Table of Contents
12 is 15 Percent of What? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from managing personal finances to analyzing business data. Understanding how to solve percentage problems, such as determining the original value when given a percentage and its corresponding part, is crucial for anyone aiming to improve their numerical proficiency. This article provides a comprehensive guide on solving the problem "12 is 15 percent of what," exploring multiple approaches and highlighting practical applications.
Understanding the Problem: Deconstructing "12 is 15 Percent of What?"
The question, "12 is 15 percent of what?" essentially asks us to find the whole number (the base value) of which 12 represents 15%. This is a common type of percentage problem that can be solved using several methods, each offering unique insights into the underlying mathematical principles. Before delving into the solutions, let's establish a clear understanding of the terms involved:
- Percentage: A ratio expressed as a fraction of 100. In this case, it's 15%.
- Part: The portion of the whole represented by the percentage. Here, it's 12.
- Whole: The total value or the base number we are trying to find. This is our unknown variable.
Method 1: Using the Percentage Formula
The most direct approach involves using the basic percentage formula:
Part = (Percentage/100) * Whole
In our problem:
- Part = 12
- Percentage = 15
- Whole = x (the unknown value we need to find)
Substituting these values into the formula:
12 = (15/100) * x
Now, we solve for x:
- Multiply both sides by 100: 1200 = 15x
- Divide both sides by 15: x = 1200 / 15
- Therefore, x = 80
Therefore, 12 is 15 percent of 80.
Method 2: Using Proportions
Another effective method utilizes the concept of proportions. We can set up a proportion relating the part to the whole:
12/x = 15/100
This proportion states that the ratio of the part (12) to the whole (x) is equal to the ratio of the percentage (15) to 100. To solve this proportion:
- Cross-multiply: 12 * 100 = 15 * x
- Simplify: 1200 = 15x
- Divide both sides by 15: x = 80
Again, we find that 12 is 15 percent of 80. This method reinforces the equivalence between the percentage formula and proportional reasoning.
Method 3: Using the Decimal Equivalent
Percentages can also be expressed as decimals. 15% is equivalent to 0.15 (obtained by dividing 15 by 100). We can rewrite the problem as:
12 = 0.15 * x
Solving for x:
- Divide both sides by 0.15: x = 12 / 0.15
- Therefore, x = 80
This method demonstrates the interchangeability between percentage, fraction, and decimal representations. It's a concise approach particularly useful when working with calculators.
Practical Applications of Percentage Calculations
The ability to solve percentage problems, as exemplified by "12 is 15 percent of what," is essential in various real-world scenarios:
1. Finance and Budgeting:
- Calculating original prices: If you bought an item on sale for $12, and the discount was 15%, you can use this method to determine the original price ($80).
- Understanding interest rates: Calculating interest earned or paid on investments or loans often involves percentage calculations.
- Analyzing investment returns: Determining the return on investment (ROI) requires calculating percentages of profit or loss.
- Tax calculations: Calculating sales tax, income tax, or other taxes involves understanding and applying percentage rates.
2. Business and Economics:
- Market share analysis: Businesses use percentages to track their market share relative to competitors.
- Profit margin calculations: Determining the profit margin involves calculating the percentage of profit relative to revenue.
- Sales growth analysis: Companies analyze percentage changes in sales figures over time to assess growth trends.
- Cost-benefit analysis: Evaluating the cost-effectiveness of projects often requires comparing costs and benefits expressed as percentages.
3. Science and Statistics:
- Data analysis: Scientists use percentages to represent data proportions and trends in their research.
- Probability calculations: Expressing probabilities often involves percentages.
- Statistical significance testing: Statistical tests use percentages to determine the significance of observed effects.
4. Everyday Life:
- Tip calculations: Determining the appropriate tip amount in restaurants involves calculating percentages of the bill.
- Discount calculations: Understanding sales discounts requires calculating percentages of the original price.
- Recipe adjustments: Scaling recipes up or down involves adjusting ingredient quantities based on percentages.
Expanding Your Percentage Skills: Beyond the Basics
While this article focuses on solving "12 is 15 percent of what," mastering percentage calculations extends beyond this specific problem. To improve your overall proficiency, consider exploring these related concepts:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values. For instance, finding the percentage increase from 50 to 60.
- Calculating percentage points: This refers to the arithmetic difference between two percentages. For example, an increase from 10% to 15% is a 5-percentage-point increase.
- Working with compound percentages: This involves applying percentages multiple times, such as calculating compound interest.
By practicing these diverse aspects of percentage calculations, you'll develop a strong foundation for handling various numerical challenges in your personal and professional life.
Conclusion: Mastering Percentages – A Valuable Skill
The ability to solve percentage problems, such as "12 is 15 percent of what," is a versatile and highly valuable skill. Understanding the underlying principles and applying different solution methods allows you to tackle a wide array of practical situations. From managing personal finances to analyzing complex data sets, proficiency in percentage calculations is a cornerstone of numerical literacy, providing a significant advantage in navigating the quantitative aspects of the modern world. By consistently practicing and expanding your knowledge of percentage concepts, you can enhance your problem-solving abilities and make informed decisions based on numerical information.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 15 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.