12 Is 15 Percent Of What Number
News Co
Mar 21, 2025 · 4 min read
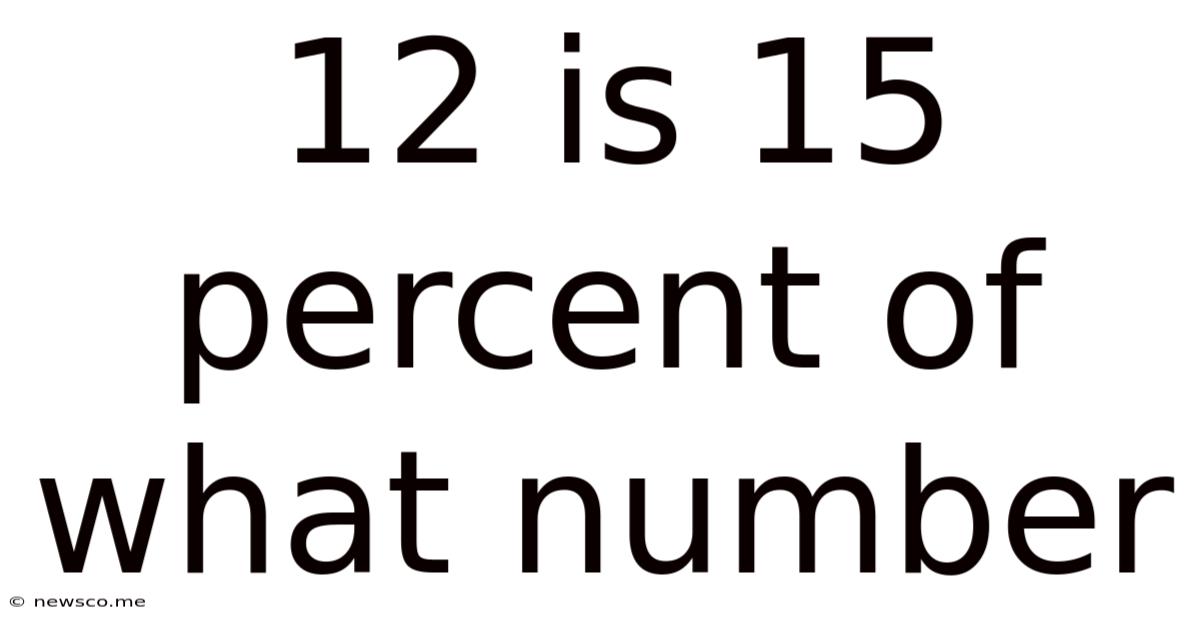
Table of Contents
12 is 15 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many areas of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into the question, "12 is 15 percent of what number?" We'll explore various methods to solve this problem, discuss the underlying principles of percentage calculations, and offer practical applications to solidify your understanding.
Understanding Percentages: The Basics
Before diving into the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" represents "percent," meaning "per hundred." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Percentages are used extensively because they provide a standardized way to compare different quantities and proportions. They simplify the interpretation of data and make it easier to understand complex relationships between numbers.
Method 1: Using the Percentage Formula
The most common way to solve percentage problems is by using the basic percentage formula:
Part = Percentage × Whole
In our problem, we know the "Part" (12) and the "Percentage" (15%). We need to find the "Whole" number. Let's rearrange the formula to solve for the "Whole":
Whole = Part / Percentage
Now, substitute the values we know:
Whole = 12 / 0.15
Remember to convert the percentage (15%) to a decimal (0.15) before performing the calculation. Dividing 12 by 0.15 gives us:
Whole = 80
Therefore, 12 is 15 percent of 80.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion to represent the problem as follows:
12 / x = 15 / 100
Where 'x' represents the unknown number we are trying to find. To solve for 'x', we can cross-multiply:
12 × 100 = 15 × x
1200 = 15x
Now, divide both sides of the equation by 15:
x = 1200 / 15
x = 80
Again, we find that 12 is 15 percent of 80.
Method 3: Using the Concept of "One Percent"
This method is particularly helpful for understanding the underlying relationship between the percentage and the whole number. If 15% of a number is 12, then 1% of that number would be:
1% = 12 / 15 = 0.8
Since there are 100% in the whole, we can find the whole number by multiplying the value of 1% by 100:
Whole = 0.8 × 100 = 80
This method demonstrates that understanding the value of 1% allows you to easily determine the whole.
Practical Applications of Percentage Calculations
The ability to solve percentage problems is crucial in numerous everyday situations, including:
-
Shopping: Calculating discounts, sales tax, and total costs after discounts. For instance, if a shirt is 20% off its original price, understanding percentages helps you determine the final price.
-
Finance: Determining interest rates, loan repayments, and investment returns. Calculating compound interest relies heavily on percentage calculations.
-
Data Analysis: Interpreting data presented as percentages, such as market share, survey results, and statistical reports. Understanding percentages provides a clear picture of proportions and trends.
-
Cooking and Baking: Scaling recipes up or down by adjusting ingredient quantities based on percentage changes. If you want to make half a recipe, you need to adjust the ingredients by 50%.
-
Science: Expressing concentrations, experimental results, and statistical probabilities as percentages. Scientific research often uses percentages to represent significant data.
Beyond the Basics: More Complex Percentage Problems
While the problem "12 is 15 percent of what number?" is relatively straightforward, percentage calculations can become more complex. Consider these scenarios:
-
Finding the percentage increase or decrease: Calculating the percentage change between two numbers requires understanding the difference between them relative to the original number.
-
Calculating compound interest: This involves calculating interest on both the principal amount and accumulated interest over multiple periods.
-
Working with multiple percentages: Some problems might involve applying multiple percentages sequentially, such as adding sales tax after a discount.
Tips and Tricks for Solving Percentage Problems
-
Always convert percentages to decimals: This simplifies calculations and reduces errors. To convert a percentage to a decimal, divide the percentage by 100.
-
Check your work: Use estimation to verify the reasonableness of your answer. Does the answer seem logical within the context of the problem?
-
Practice regularly: The more you practice, the more comfortable and efficient you will become with percentage calculations. Use online calculators, worksheets, and real-life examples to hone your skills.
-
Understand the context: Pay attention to the wording of the problem to ensure you are applying the correct formula and solving for the correct variable.
Conclusion: Mastering Percentage Calculations
Understanding how to solve problems like "12 is 15 percent of what number?" is a valuable skill with widespread applications. By mastering the various methods discussed – using the percentage formula, setting up proportions, and working with the concept of "one percent" – you'll develop a strong foundation for tackling a wide range of percentage-related problems. Regular practice and a clear understanding of the underlying principles will ensure your success in navigating this essential aspect of mathematics and its real-world applications. Remember to always check your work and consider the practical implications of your calculations to ensure accuracy and relevance.
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 Is 15 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.