12 Is What Percent Of 60
News Co
Mar 29, 2025 · 4 min read
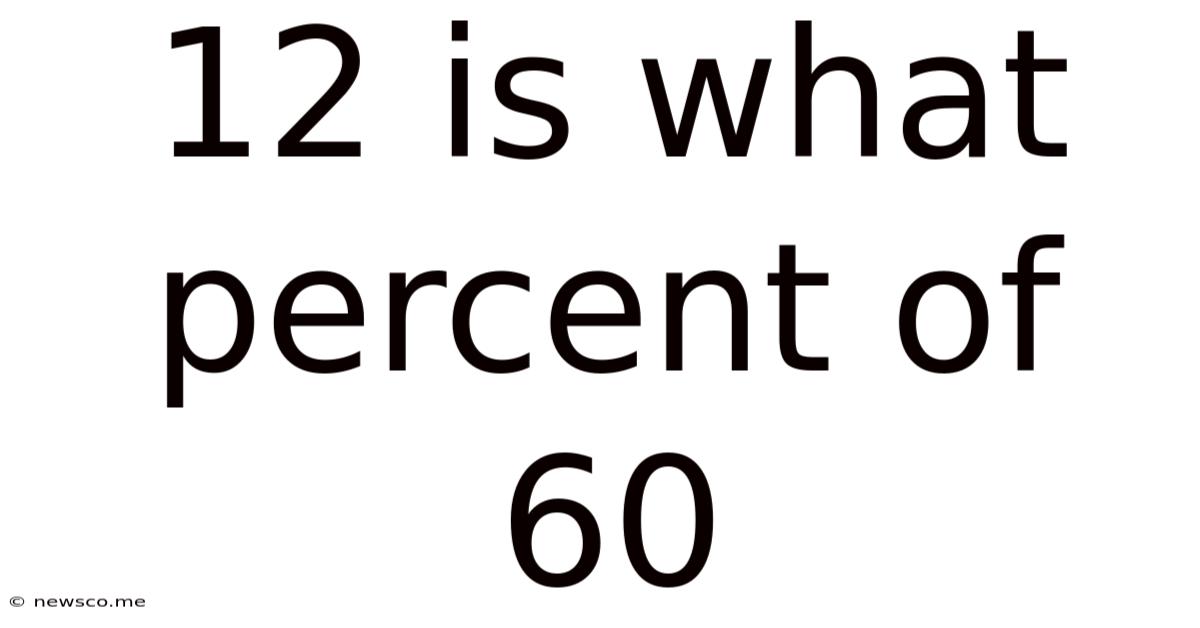
Table of Contents
12 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to solve percentage problems, such as determining "12 is what percent of 60?", is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and tools to tackle similar percentage calculations with confidence.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Percentage Formula
The most common method for solving percentage problems involves using a straightforward formula:
(Part / Whole) * 100 = Percentage
In our problem, "12 is what percent of 60?", we can identify:
- Part: 12 (the number we want to express as a percentage of the whole)
- Whole: 60 (the total amount)
Substituting these values into the formula:
(12 / 60) * 100 = Percentage
Simplifying the fraction:
(1/5) * 100 = 20
Therefore, 12 is 20% of 60.
Method 2: Using Proportions
Another effective approach to solving percentage problems is by setting up a proportion. A proportion is an equation that states that two ratios are equal. We can represent the problem as:
12/60 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
12 * 100 = 60 * x
1200 = 60x
x = 1200 / 60
x = 20
Again, this confirms that 12 is 20% of 60.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
- Convert the fraction: Express the part as a fraction of the whole: 12/60.
- Simplify the fraction: Reduce the fraction to its simplest form: 1/5.
- Convert to decimal: Divide the numerator by the denominator: 1 ÷ 5 = 0.2
- Convert to percentage: Multiply the decimal by 100: 0.2 * 100 = 20%
This method reinforces that 12 is 20% of 60.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is invaluable in various real-life scenarios:
Finance:
- Calculating discounts: If a store offers a 25% discount on a $100 item, you can easily calculate the discount amount and the final price using percentage calculations.
- Determining interest rates: Understanding interest rates on loans, savings accounts, and investments requires a solid grasp of percentages.
- Analyzing financial statements: Analyzing profit margins, revenue growth, and expense ratios involves extensive use of percentage calculations.
- Calculating taxes: Income tax, sales tax, and other taxes are often expressed as percentages.
Science:
- Expressing experimental results: Scientific data is frequently presented as percentages, such as the percentage of successful trials in an experiment or the percentage composition of a chemical compound.
- Analyzing statistical data: Percentages are used extensively in statistical analyses to represent proportions, probabilities, and other key metrics.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount at restaurants involves calculating a percentage of the bill.
- Understanding surveys and polls: Interpreting results from surveys and polls often involves analyzing percentages.
- Comparing prices: Comparing the prices of different products or services frequently necessitates comparing percentages.
- Tracking progress towards goals: Monitoring progress towards personal goals, such as weight loss or saving money, often involves tracking progress as percentages.
Advanced Percentage Problems and Their Solutions
While the problem "12 is what percent of 60?" is relatively straightforward, let's explore some more complex percentage problems and their solutions:
Problem 1: What is 15% of 80?
Using the formula: (15/100) * 80 = 12
Problem 2: 25 is what percent of 50?
(25/50) * 100 = 50%
Problem 3: 30 is 20% of what number?
Let 'x' represent the unknown number:
30 = (20/100) * x
30 = 0.2x
x = 30 / 0.2
x = 150
Tips for Mastering Percentage Calculations
- Practice regularly: The key to mastering percentage calculations is consistent practice. Try solving different types of percentage problems to build your skills and confidence.
- Use multiple methods: Experiment with different methods, such as using the formula, proportions, or decimal conversions, to find the approach that best suits your understanding.
- Visual aids: Use diagrams or charts to visualize the problem and understand the relationships between the parts and the whole.
- Check your work: Always double-check your calculations to ensure accuracy.
- Break down complex problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps.
Conclusion
Understanding how to calculate percentages is a valuable skill that has numerous applications in various aspects of life. By mastering the different methods and consistently practicing, you can confidently solve a wide range of percentage problems, from simple calculations to more complex scenarios. Remember the fundamental formula, (Part / Whole) * 100 = Percentage, and you'll be well-equipped to handle any percentage calculation you encounter. This guide provided multiple methods to solve "12 is what percent of 60?" (the answer is 20%), and equips you with the tools to confidently tackle future percentage challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.