14 Divided By 3 With Remainder
News Co
May 07, 2025 · 5 min read
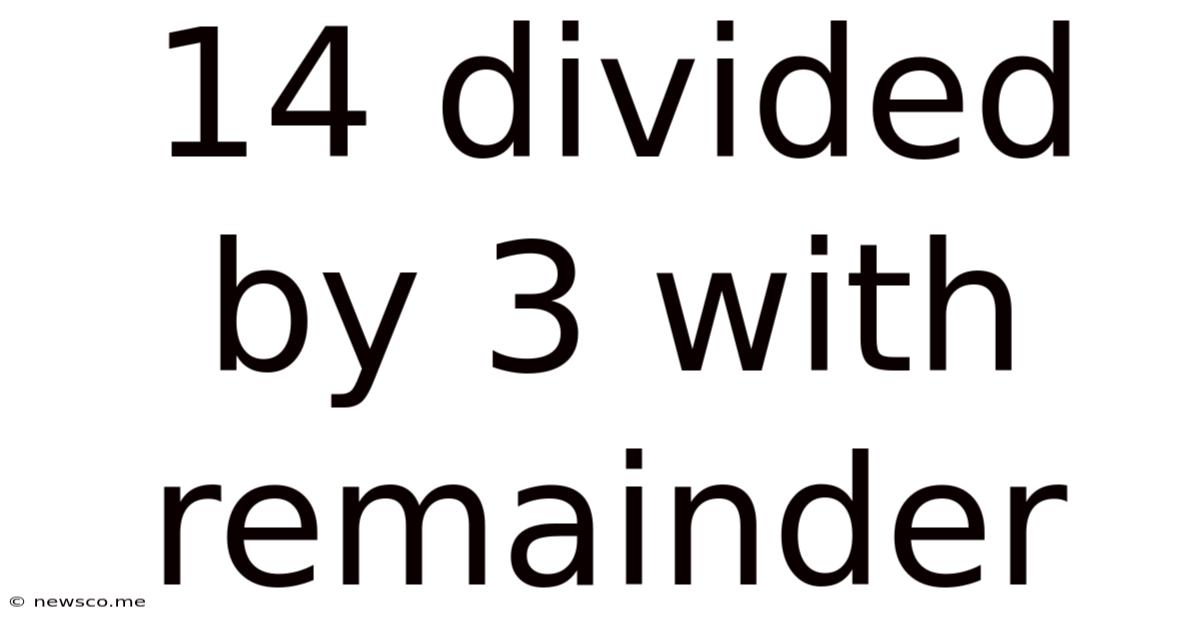
Table of Contents
14 Divided by 3: Understanding Remainders and Their Applications
The seemingly simple question, "What is 14 divided by 3?", opens a door to a fundamental concept in mathematics: division with remainders. While a calculator might readily provide the decimal answer (approximately 4.667), understanding the remainder is crucial for various mathematical applications and problem-solving scenarios. This article delves deep into this concept, exploring its meaning, practical uses, and connections to other mathematical ideas.
Understanding Division with Remainders
Division, at its core, is about splitting a quantity into equal parts. When dividing 14 by 3, we're trying to figure out how many groups of 3 we can make from 14. We can create four such groups (4 x 3 = 12), but we'll have 2 left over. This "leftover" is the remainder.
In the expression 14 ÷ 3 = 4 R 2:
- 14 is the dividend (the number being divided).
- 3 is the divisor (the number we're dividing by).
- 4 is the quotient (the number of times the divisor goes into the dividend completely).
- 2 is the remainder (the amount left over after the division).
This representation, using "R" to denote the remainder, is a clear and concise way to express the result of division when the dividend isn't perfectly divisible by the divisor. This concept extends beyond simple arithmetic and finds its applications in various fields.
The Algorithm and its Steps: A Detailed Look
The process of finding the quotient and remainder involves a series of steps that form a fundamental algorithm in arithmetic. Let's break down the process of dividing 14 by 3 step-by-step:
-
Identify the Dividend and Divisor: We have a dividend of 14 and a divisor of 3.
-
Repeated Subtraction: We repeatedly subtract the divisor (3) from the dividend (14) until the result is less than the divisor.
- 14 - 3 = 11
- 11 - 3 = 8
- 8 - 3 = 5
- 5 - 3 = 2
-
Count the Subtractions: We subtracted 3 a total of four times. This is our quotient (4).
-
Identify the Remainder: The final result after repeated subtraction is 2. This is our remainder.
-
Express the Result: We can express the result as 14 ÷ 3 = 4 R 2.
This method, while seemingly simple for small numbers, lays the groundwork for understanding more complex division algorithms used in computers and other systems.
Applications of Remainders: Beyond Basic Arithmetic
The concept of remainders extends far beyond simple arithmetic problems. Its applications span various fields, including:
1. Modular Arithmetic (Clock Arithmetic):
Imagine a 12-hour clock. If it's currently 8 o'clock and you add 6 hours, you'll end up at 2 o'clock. This is because 8 + 6 = 14, and 14 divided by 12 leaves a remainder of 2. Modular arithmetic uses remainders to handle cyclical patterns, making it crucial in cryptography and computer science.
2. Data Structures and Algorithms:
Remainders play a crucial role in data structures like hash tables. Hash tables use a hash function to assign data elements to locations in an array. The remainder from a division operation often determines which array location a particular data element will occupy. This efficient allocation allows for faster data retrieval.
3. Scheduling and Time Management:
Consider scheduling tasks that repeat every 3 days. If you start on day 14, calculating the remainder when 14 is divided by 3 will tell you which day of the cycle the task will fall on (remainder 2, meaning the second day of the 3-day cycle).
4. Number Theory and Cryptography:
Remainders are fundamental in number theory, particularly in concepts like modular arithmetic, which is the basis for many encryption algorithms used to secure online communication. The properties of remainders are used to create sophisticated mathematical puzzles and systems for secure data transmission.
5. Geometry and Measurement:
Remainders appear in geometrical calculations. For instance, if you need to cut a 14-meter rope into 3-meter pieces, the remainder represents the length of the leftover piece.
6. Real-World Problem Solving:
Imagine you have 14 apples and want to distribute them equally among 3 friends. The quotient tells you each friend gets 4 apples, and the remainder tells you you'll have 2 apples left over.
Connecting Remainders to Other Mathematical Concepts
The concept of remainders is intricately linked to other mathematical concepts:
1. Fractions and Decimals:
The remainder can be expressed as a fraction: 14 ÷ 3 = 4 2/3. This fraction can then be converted into a decimal (approximately 4.667). Understanding remainders helps in understanding the relationship between fractions, decimals, and whole numbers.
2. Long Division:
The long division algorithm explicitly calculates the quotient and remainder. Understanding remainders is essential for mastering the long division process.
3. Prime Numbers and Divisibility:
The concept of remainders is closely related to prime numbers and divisibility rules. A number is divisible by another only if the remainder is 0 when divided. This is a foundation for understanding prime factorization.
Beyond 14 Divided by 3: Exploring Different Scenarios
While we've focused on 14 divided by 3, the concept of remainders applies to any division problem where the dividend is not perfectly divisible by the divisor. Let's explore a few more examples:
- 25 ÷ 4 = 6 R 1: Twenty-five divided by four gives a quotient of 6 and a remainder of 1.
- 37 ÷ 7 = 5 R 2: Thirty-seven divided by seven gives a quotient of 5 and a remainder of 2.
- 100 ÷ 11 = 9 R 1: One hundred divided by eleven gives a quotient of 9 and a remainder of 1.
These examples highlight the versatility and importance of understanding remainders in various mathematical contexts.
Conclusion: The Significance of Remainders
The seemingly simple problem of 14 divided by 3 reveals the profound significance of remainders in mathematics and its various applications. Understanding remainders is not just about solving basic division problems; it's about grasping a fundamental concept that underpins advanced mathematical principles, algorithm design, and real-world problem-solving. From modular arithmetic and cryptography to scheduling and data structures, the remainder plays a vital role in many aspects of our lives and the digital world around us. Its seemingly simple presence belies its remarkable power and influence across diverse fields. By comprehending the meaning and applications of remainders, we unlock a deeper understanding of the mathematical fabric of our world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 14 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.