15 Is 20 Of What Number
News Co
Apr 19, 2025 · 5 min read
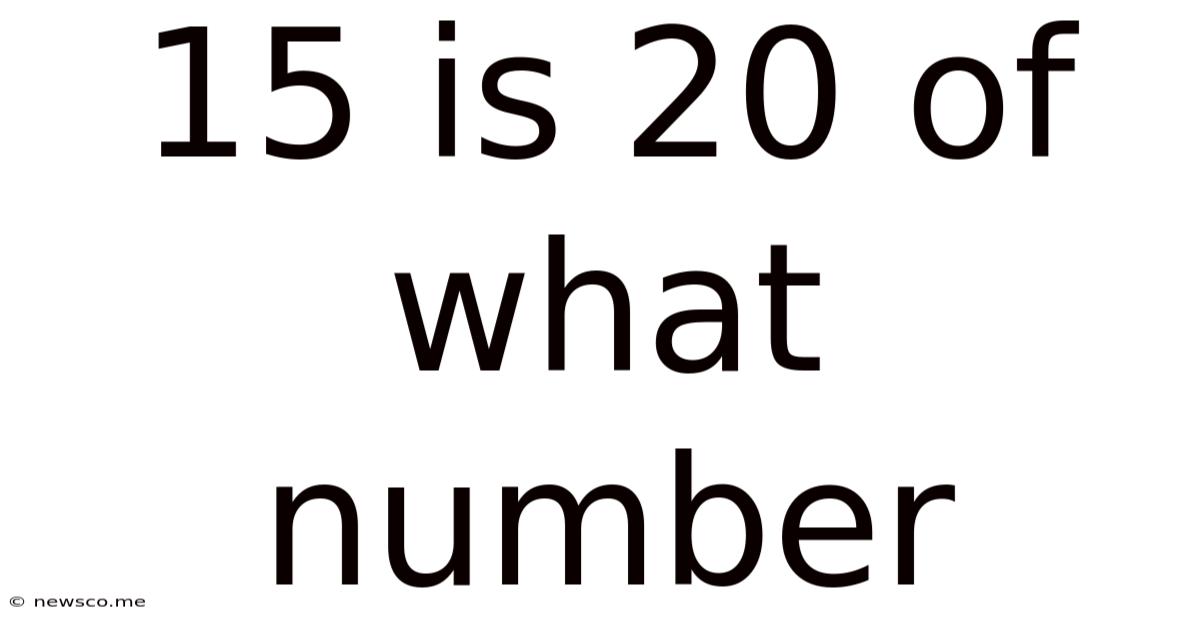
Table of Contents
15 is 20% of What Number? A Deep Dive into Percentage Calculations
Finding out what number 15 represents 20% of is a common problem encountered in various fields, from everyday budgeting to complex financial analyses. Understanding how to solve this kind of percentage problem is crucial for anyone looking to improve their numeracy skills and problem-solving abilities. This article will guide you through several methods of solving this problem, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore both the algebraic approach and the practical application of this concept, equipping you with the tools to tackle similar percentage calculations with confidence.
Understanding Percentages
Before diving into the solution, let's revisit the fundamental concept of percentages. A percentage is simply a fraction expressed as a part of 100. For instance, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. This representation is crucial for understanding how percentages relate to the whole.
Method 1: The Algebraic Approach
This method employs a straightforward algebraic equation to solve for the unknown number. Let's represent the unknown number as 'x'. The problem "15 is 20% of what number?" can be translated into the following equation:
15 = 0.20 * x
Here's how to solve it step-by-step:
-
Convert the percentage to a decimal: 20% is equivalent to 0.20 (divide the percentage by 100).
-
Substitute into the equation: This gives us 15 = 0.20x.
-
Isolate 'x': To isolate 'x', divide both sides of the equation by 0.20:
x = 15 / 0.20
-
Calculate the result: Performing the division, we find:
x = 75
Therefore, 15 is 20% of 75.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as:
15/x = 20/100
This proportion states that the ratio of 15 to the unknown number (x) is equal to the ratio of 20 to 100. To solve this proportion:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa:
15 * 100 = 20 * x
-
Simplify: This simplifies to:
1500 = 20x
-
Solve for 'x': Divide both sides by 20:
x = 1500 / 20
-
Calculate the result:
x = 75
Again, we find that 15 is 20% of 75.
Method 3: Working Backwards from the Percentage
This method relies on understanding the relationship between the percentage and the whole. If 15 represents 20%, then we can find the value of 1% by dividing 15 by 20:
1% = 15 / 20 = 0.75
Since 1% represents 0.75, to find the value of 100% (the whole number), we simply multiply 0.75 by 100:
100% = 0.75 * 100 = 75
This confirms that 15 is 20% of 75.
Practical Applications: Real-World Scenarios
Understanding percentage calculations is essential in various real-life situations. Here are some examples:
1. Sales and Discounts:
Imagine a store offers a 20% discount on an item originally priced at $75. The discount amount would be 20% of $75, which is $15. This leaves the final price at $60. The calculations we've explored show how to work this out both ways - finding the discount amount given the original price and percentage, or finding the original price given the discount amount and percentage.
2. Financial Calculations:
Percentage calculations are frequently used in finance. For example, calculating interest earned on savings accounts, determining the amount of tax payable, or understanding the return on investment (ROI) all involve percentage computations. If you received $15 interest which represents 20% of your total investment, your initial investment was $75.
3. Data Analysis:
In data analysis and statistics, percentages are used to represent proportions and trends within datasets. For example, if 15 out of 100 survey respondents answered 'yes' to a question, this translates to a 15% response rate. Understanding this relationship allows analysts to draw meaningful conclusions from data.
4. Everyday Budgeting:
Budgeting involves careful tracking of income and expenses. Knowing the percentage of your income spent on certain categories (like housing, transportation, or food) helps you manage your finances effectively. For instance, if 20% of your monthly income is allocated to savings, and you save $15, this tells you your total monthly income.
Expanding Your Skills: Variations on the Problem
While the core problem focuses on finding the whole number when given a percentage and a part, let's explore some related percentage problems to broaden your understanding:
- Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, what percentage is 15 of 75? (The answer is 20%).
- Finding the part: If you know the whole and the percentage, you can calculate the part. For example, what is 20% of 75? (The answer is 15).
- Problems with multiple percentages: You might encounter scenarios involving more than one percentage calculation. For example, if an item is discounted by 20% and then an additional 10%, the final price will be determined by calculating the percentages successively.
Mastering these variations ensures you're equipped to tackle a wide range of percentage problems confidently.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems like "15 is 20% of what number?" is a valuable skill that transcends academic settings and finds application in everyday life and various professional contexts. By understanding the underlying principles and employing the different methods discussed – the algebraic approach, proportions, and working backward – you can approach such problems with confidence and accuracy. Remember to practice regularly and explore different variations to further solidify your understanding and enhance your problem-solving prowess. The more you practice, the more intuitive these calculations will become. This will undoubtedly benefit you in various aspects of your life, from personal finance to professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about 15 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.