15 Is 20 Percent Of What
News Co
Apr 14, 2025 · 4 min read
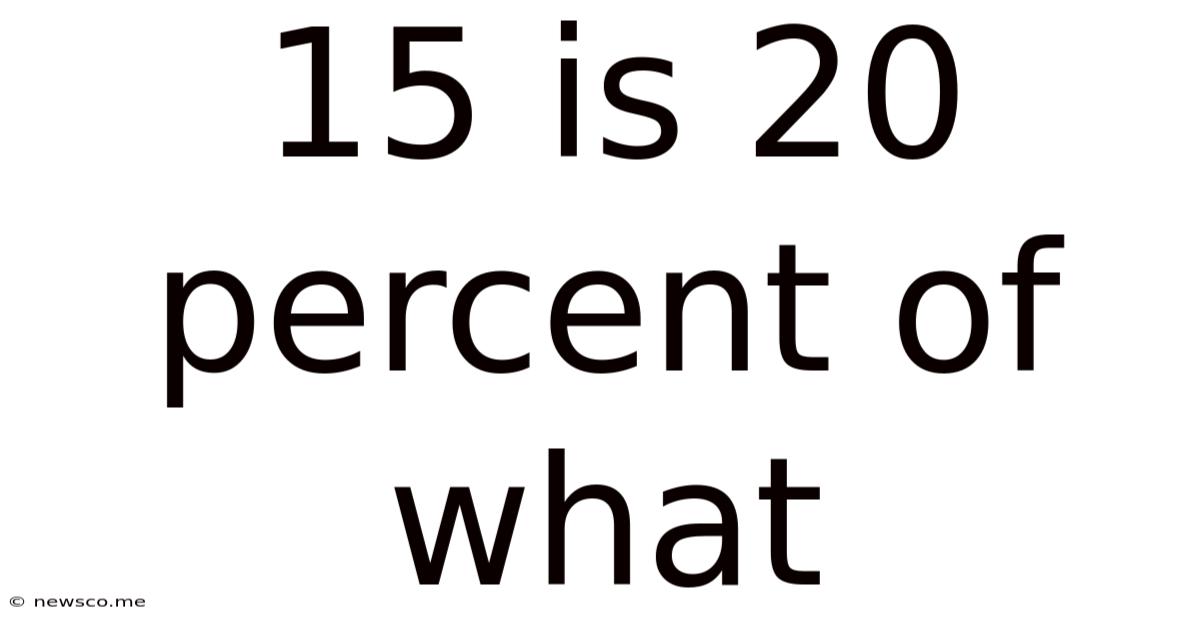
Table of Contents
15 is 20 Percent of What: A Comprehensive Guide to Percentage Calculations
Determining what number 15 represents 20% of is a fundamental percentage problem. This seemingly simple question opens the door to understanding a crucial mathematical concept with widespread applications in various fields, from finance and budgeting to sales and statistics. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, providing you with the tools to solve similar percentage problems independently.
Understanding Percentages
Before diving into the specifics of calculating the original number, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." For instance, 20% can be written as:
- A fraction: 20/100 (which simplifies to 1/5)
- A decimal: 0.20
Solving "15 is 20 Percent of What?"
The core of this problem lies in understanding the relationship between the percentage, the part, and the whole. We're given:
- The part: 15
- The percentage: 20%
We need to find the whole. We can express this relationship mathematically as an equation:
20% * x = 15
Where 'x' represents the unknown whole number. To solve for 'x', we'll follow these steps:
Step 1: Convert the Percentage to a Decimal
As mentioned earlier, 20% is equivalent to 0.20. Substituting this into our equation, we get:
0.20 * x = 15
Step 2: Isolate the Variable
To isolate 'x', we need to divide both sides of the equation by 0.20:
x = 15 / 0.20
Step 3: Calculate the Result
Performing the division, we find:
x = 75
Therefore, 15 is 20% of 75.
Alternative Methods: Using Proportions
Another effective approach involves using proportions. Proportions establish an equivalence between two ratios. We can set up a proportion as follows:
20/100 = 15/x
This proportion states that 20 out of 100 is equivalent to 15 out of 'x'. To solve for 'x', we can cross-multiply:
20x = 15 * 100
20x = 1500
x = 1500 / 20
x = 75
This method confirms our previous result: 15 is 20% of 75.
Real-World Applications: Percentage Calculations in Daily Life
Percentage calculations are ubiquitous in everyday life. Here are several scenarios where understanding this concept is crucial:
1. Finance and Budgeting:
- Interest Rates: Calculating simple or compound interest on loans, savings accounts, or investments involves percentage calculations. For instance, determining the interest earned on a savings account with a certain annual interest rate.
- Discounts and Sales: Understanding discounts offered during sales requires calculating percentages. If a product is discounted by 25%, knowing how to determine the final price is essential.
- Taxes: Calculating sales tax, income tax, or property tax involves determining percentages of income or purchase price.
- Tips and Gratuities: Calculating tips in restaurants or service charges often involves calculating a percentage of the total bill.
2. Sales and Marketing:
- Sales Growth: Tracking sales growth over time often involves calculating percentage changes. This helps analyze trends and performance.
- Market Share: Determining market share involves comparing sales figures as percentages of the total market size.
- Conversion Rates: In online marketing, conversion rates track the percentage of website visitors who complete a desired action (e.g., making a purchase).
- Profit Margins: Businesses use percentage calculations to determine their profit margin—the percentage of revenue remaining after deducting costs.
3. Statistics and Data Analysis:
- Data Representation: Percentages are frequently used to represent data in charts, graphs, and reports to make it easier to understand.
- Probability: Calculating probabilities involves determining the likelihood of events occurring as percentages.
- Sampling: In statistical sampling, percentages are used to represent the proportion of a sample that possesses certain characteristics.
Beyond the Basics: Advanced Percentage Problems
While the "15 is 20 percent of what?" problem is a fundamental introduction, more complex scenarios can arise:
- Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two numbers.
- Calculating Percentages of Percentages: This can be encountered in situations involving compound interest or discounts applied sequentially.
- Solving Problems with Multiple Percentages: Some problems might involve multiple percentages applied simultaneously or sequentially, requiring careful consideration of the order of operations.
Mastering Percentage Calculations: Tips and Tricks
To become proficient in percentage calculations:
- Practice Regularly: The key to mastering any mathematical concept is consistent practice. Solve various percentage problems to improve your understanding and speed.
- Use Different Methods: Experiment with various approaches—like using proportions or equations—to find the method that best suits your understanding.
- Visualize the Problem: Representing percentage problems visually, such as with diagrams or charts, can enhance understanding.
- Check Your Answers: Always verify your calculations to ensure accuracy.
Conclusion: The Power of Percentages
The seemingly simple question, "15 is 20 percent of what?" reveals the profound significance of percentage calculations in our daily lives. By understanding the underlying principles and mastering various solution methods, you equip yourself with a powerful tool applicable across a broad spectrum of fields. From managing personal finances to analyzing business performance or understanding statistical data, the ability to work confidently with percentages is an invaluable skill. The more you practice, the more intuitive and effortless these calculations will become, paving the way for a deeper understanding of numerical relationships in the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 15 Is 20 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.