15 Is 20 Percent Of What Number
News Co
May 07, 2025 · 4 min read
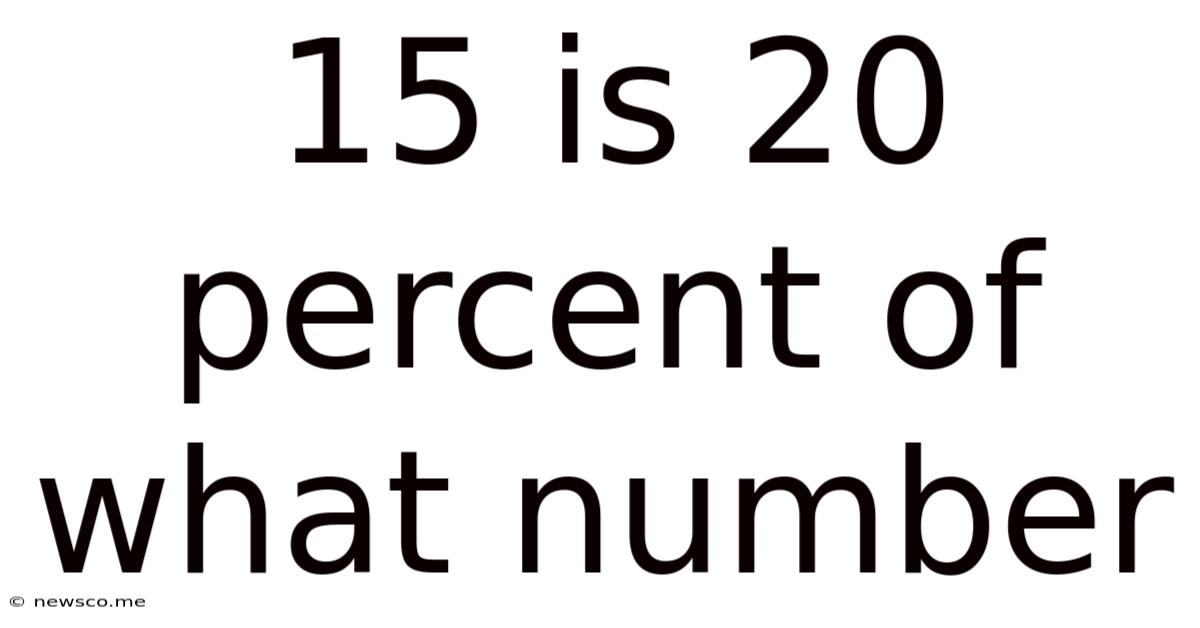
Table of Contents
15 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "15 is 20 percent of what number?", exploring multiple methods to solve this type of percentage problem and providing a solid foundation for tackling similar calculations. We'll also explore the broader application of percentage calculations and offer practical tips for improving your proficiency.
Understanding the Problem: Deconstructing "15 is 20 Percent of What Number?"
The core of this problem lies in understanding the relationship between a percentage, a part, and a whole. We are given a part (15), a percentage (20%), and we need to find the whole number. This is a common percentage problem, and solving it involves applying the principles of percentage calculations.
The question can be visually represented as follows:
20% of X = 15
Where 'X' represents the unknown number we are trying to find.
Method 1: Using the Equation Method
This method is based on converting the percentage into a decimal and setting up an algebraic equation. Here's how it works:
-
Convert the percentage to a decimal: 20% is equivalent to 0.20 (divide the percentage by 100).
-
Set up the equation: The problem can be expressed as: 0.20 * X = 15
-
Solve for X: To isolate X, divide both sides of the equation by 0.20:
X = 15 / 0.20
-
Calculate the result: X = 75
Therefore, 15 is 20 percent of 75.
Method 2: Using the Proportion Method
The proportion method utilizes the concept of ratios to solve the problem. It's particularly useful for visualizing the relationship between the parts and the whole.
-
Set up the proportion: We can set up a proportion as follows:
20/100 = 15/X
This represents the ratio of the percentage to the whole (20/100) being equal to the ratio of the part to the whole (15/X).
-
Cross-multiply: Cross-multiply the terms to solve for X:
20 * X = 15 * 100
-
Simplify and solve:
20X = 1500 X = 1500 / 20 X = 75
Again, we find that 15 is 20 percent of 75.
Method 3: Using the Percentage Formula
A more generalized approach involves using the basic percentage formula:
Part / Whole = Percentage / 100
Substituting the known values:
15 / X = 20 / 100
Cross-multiplying and solving for X will yield the same result: X = 75.
Practical Applications of Percentage Calculations
Understanding how to solve percentage problems is crucial in many real-world scenarios. Here are a few examples:
-
Calculating discounts: If a store offers a 20% discount on an item priced at $75, you can easily calculate the discount amount ($15) and the final price ($60).
-
Determining tax amounts: Knowing the sales tax percentage allows you to calculate the total cost of an item, including taxes.
-
Analyzing financial statements: Percentage changes in revenue, profit, and other financial metrics are vital for assessing business performance.
-
Understanding statistical data: Percentages are commonly used to represent data in graphs, charts, and reports, helping to visualize and interpret information.
-
Calculating tips and gratuities: Figuring out a tip at a restaurant often involves calculating a percentage of the total bill.
Tips for Improving Your Percentage Calculation Skills
-
Master the basics: Ensure you thoroughly understand the relationship between percentages, decimals, and fractions.
-
Practice regularly: Solving various percentage problems regularly will improve your speed and accuracy.
-
Use different methods: Try different approaches (equation, proportion, formula) to find the method that suits you best.
-
Check your work: Always double-check your calculations to avoid errors.
-
Utilize online calculators: While it's important to understand the underlying principles, online calculators can help verify your answers.
Beyond the Basics: More Complex Percentage Problems
While the problem "15 is 20 percent of what number?" is relatively straightforward, percentage calculations can become more complex. Here are some examples:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two numbers.
-
Calculating compound interest: Compound interest involves earning interest on both the principal and accumulated interest.
-
Solving problems with multiple percentages: Some problems might involve applying multiple percentages sequentially or simultaneously.
-
Working with percentages of percentages: Understanding how to calculate percentages of percentages is crucial in certain applications, such as calculating discounts within discounts.
Conclusion: Mastering the Art of Percentage Calculations
The ability to solve percentage problems efficiently and accurately is a valuable asset. By understanding the different methods, practicing regularly, and exploring more advanced applications, you can build a strong foundation in percentage calculations and apply this skill to various aspects of your personal and professional life. Remember, the key is understanding the underlying concepts and practicing consistently. Through diligent effort, you'll confidently tackle any percentage problem that comes your way, just as you successfully solved the puzzle of "15 is 20 percent of what number?" This comprehensive guide has equipped you with the knowledge and tools necessary to become proficient in percentage calculations and conquer any percentage-related challenge.
Latest Posts
Related Post
Thank you for visiting our website which covers about 15 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.