15 Is What Percent Of 300
News Co
May 03, 2025 · 5 min read
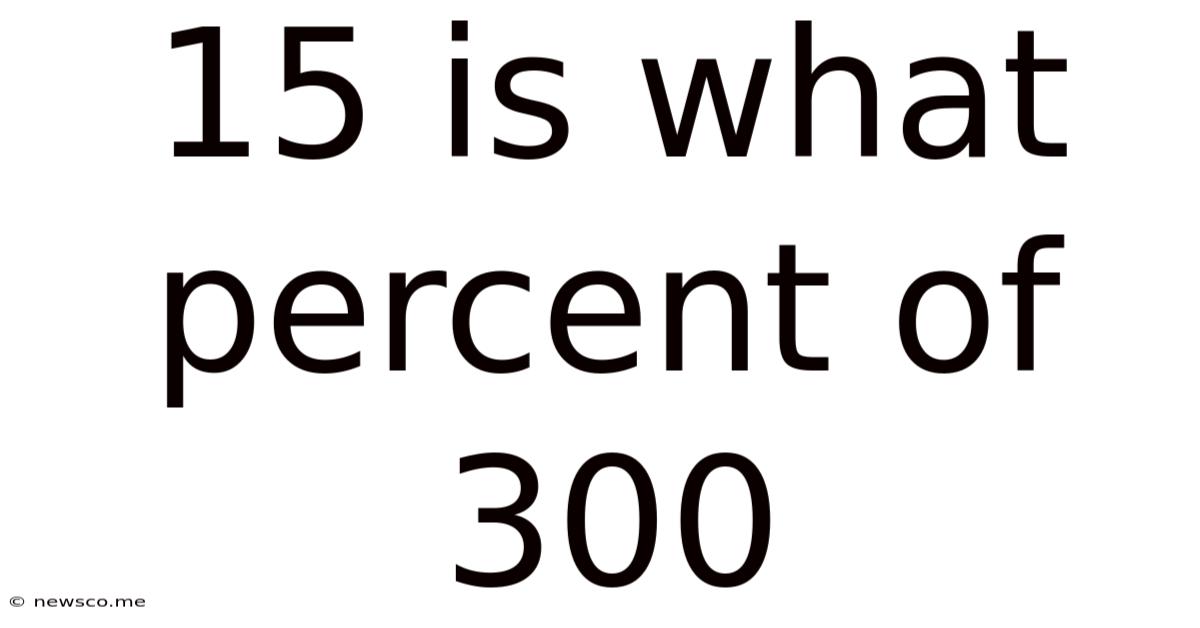
Table of Contents
15 is What Percent of 300: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into how to determine what percentage 15 represents of 300, exploring the underlying mathematical principles and providing practical applications. We'll also examine different methods for solving percentage problems, ensuring you gain a solid understanding of this crucial concept.
Understanding Percentages
Before we dive into the specific calculation, let's establish a firm grasp on what percentages actually mean. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Formula
The most straightforward method for calculating percentages involves using a basic formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 15
- Whole: 300
Substituting these values into the formula:
(15 / 300) * 100% = 5%
Therefore, 15 is 5% of 300.
Method 2: Simplifying the Fraction
Another approach involves simplifying the fraction before multiplying by 100%. This method can be particularly helpful when dealing with larger numbers or fractions that can be easily reduced.
- Form the fraction: 15/300
- Simplify the fraction: Divide both the numerator (15) and the denominator (300) by their greatest common divisor (GCD), which is 15. This simplifies the fraction to 1/20.
- Convert to a percentage: (1/20) * 100% = 5%
This method confirms our earlier result: 15 is 5% of 300.
Method 3: Using Proportions
Proportions offer a slightly different yet equally effective approach to solving percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion to solve our problem:
15/300 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
15 * 100 = 300 * x
1500 = 300x
x = 1500 / 300
x = 5
Therefore, 15 is 5% of 300.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has numerous practical applications in everyday life and various professional fields. Here are just a few examples:
1. Retail and Sales
- Discounts: Calculating discounts on sale items is a common application. If a store offers a 20% discount on a $100 item, you can easily determine the discount amount ($20) and the final price ($80).
- Sales Tax: Determining the sales tax amount added to a purchase requires percentage calculations.
- Profit Margins: Businesses use percentage calculations to determine their profit margins, helping them make informed pricing decisions.
2. Finance and Investments
- Interest Rates: Understanding interest rates on loans and investments necessitates working with percentages. Calculating compound interest involves repeated percentage calculations.
- Returns on Investment (ROI): ROI is expressed as a percentage, reflecting the profitability of an investment.
- Financial Statements: Financial statements utilize percentages extensively to analyze key financial ratios and trends.
3. Data Analysis and Statistics
- Data Representation: Percentages are often used to represent data in charts and graphs, making it easier to visualize and interpret information.
- Statistical Analysis: Many statistical measures, such as percentages and proportions, are essential for analyzing data sets and drawing inferences.
4. Everyday Life
- Tip Calculation: Determining an appropriate tip amount in a restaurant often involves calculating a percentage of the bill.
- Recipe Adjustments: Scaling up or down recipes requires adjusting ingredient quantities based on percentages.
Advanced Percentage Calculations
While the basic percentage calculation is straightforward, there are more complex scenarios that involve multiple steps or more intricate mathematical operations. Let's explore some of these:
Finding the Whole when Given a Percentage and Part
Suppose you know that 15 represents 5% of a certain number, and you need to determine that number. We can adapt our formula:
(Part / Percentage) * 100 = Whole
(15 / 5) * 100 = 300
This confirms our initial problem: 15 is 5% of 300.
Calculating Percentage Increase or Decrease
Percentage change is frequently used to analyze trends and growth. To calculate a percentage increase or decrease, use the following formula:
[(New Value - Old Value) / Old Value] * 100%
For instance, if a stock price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
Compound Percentage Calculations
Compounding involves applying a percentage repeatedly over time. This is common in finance, where interest is compounded annually, semi-annually, or even daily. The calculations become more complex, often requiring iterative processes or specific financial formulas.
Tips for Mastering Percentage Calculations
- Practice regularly: The key to mastering percentages is consistent practice. Work through various examples and problems of increasing complexity.
- Understand the underlying concepts: Ensure you have a solid grasp of fractions, decimals, and ratios, as these are fundamental to understanding percentages.
- Use different methods: Try solving problems using multiple methods (formula, simplification, proportions) to strengthen your understanding and identify the most efficient approach for specific scenarios.
- Utilize online resources and tools: Many online calculators and resources can help you verify your calculations and learn more about percentage calculations.
- Apply percentages to real-world situations: Relate percentage calculations to practical situations in your daily life to solidify your understanding and enhance your problem-solving abilities.
Conclusion
Calculating percentages is a valuable skill applicable in countless situations. Whether it's determining discounts in a shop, analyzing financial data, or understanding statistical trends, mastering percentage calculations empowers you to make informed decisions and interpret information effectively. Through understanding the fundamental principles and practicing various methods, you can confidently tackle percentage problems of all complexities. Remember, the key is consistent practice and a strong grasp of the underlying mathematical concepts. By applying these techniques, you'll be well-equipped to navigate the world of percentages with ease and confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.