16 Is 20 Of What Number
News Co
May 09, 2025 · 5 min read
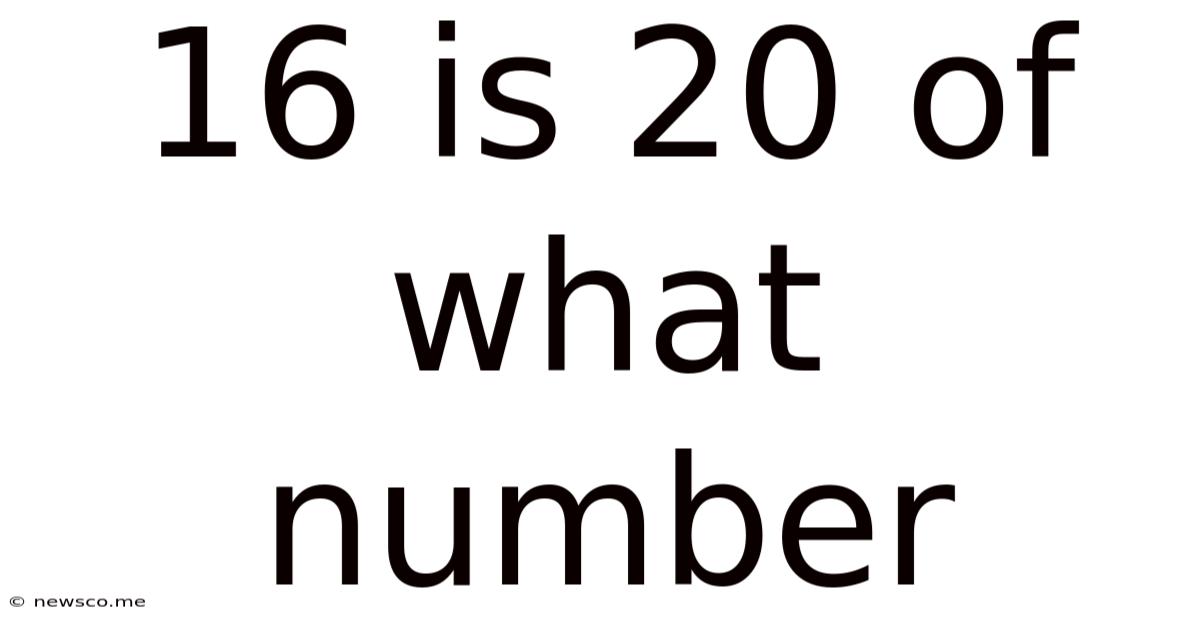
Table of Contents
16 is 20% of What Number? A Comprehensive Guide to Percentage Calculations
This article delves deep into the seemingly simple question: "16 is 20% of what number?" While the answer might seem straightforward at first glance, understanding the underlying principles of percentage calculations is crucial for various applications in mathematics, finance, and everyday life. We will not only solve this specific problem but also explore various methods and provide a comprehensive understanding of percentage calculations. This guide will equip you with the knowledge to tackle similar problems with ease and confidence.
Understanding Percentages
Before we dive into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 20% means 20 out of 100, which can also be written as the fraction 20/100 or the decimal 0.20.
Understanding this fundamental concept is key to solving percentage problems. We often encounter percentages in various contexts, including:
- Discounts and Sales: Stores often advertise discounts as percentages (e.g., 20% off).
- Taxes and Interest: Taxes and interest rates are typically expressed as percentages.
- Statistics and Data Analysis: Percentages are widely used to represent proportions and trends in data.
- Financial Calculations: Percentages are essential for calculating profits, losses, and returns on investments.
Method 1: Using the Percentage Formula
The most common way to solve percentage problems is by using the basic percentage formula:
Part = Percentage × Whole
In our problem, we know the "Part" (16) and the "Percentage" (20%). We need to find the "Whole," which we'll represent with the variable 'x'. Let's plug the known values into the formula:
16 = 0.20 × x
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.20:
x = 16 / 0.20
x = 80
Therefore, 16 is 20% of 80.
Method 2: Using Proportions
Another effective method to solve percentage problems is by setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
16/x = 20/100
This proportion states that the ratio of 16 to the unknown number (x) is equal to the ratio of 20 to 100 (which is the definition of 20%).
To solve this proportion, we can cross-multiply:
16 × 100 = 20 × x
1600 = 20x
Now, divide both sides by 20:
x = 1600 / 20
x = 80
Again, we find that 16 is 20% of 80.
Method 3: Using the Decimal Equivalent
As we mentioned earlier, percentages can be represented as decimals. 20% is equivalent to 0.20. We can use this decimal equivalent directly in the equation:
16 = 0.20x
Dividing both sides by 0.20, we get:
x = 16 / 0.20
x = 80
This method is essentially a simplified version of Method 1.
Practical Applications and Real-World Examples
Understanding percentage calculations is essential for various real-world scenarios. Let's look at a few examples:
Example 1: Sales and Discounts
A store offers a 20% discount on a product originally priced at $80. What is the discount amount?
Using the formula: Discount = 20% × $80 = 0.20 × $80 = $16. The discount amount is $16.
Example 2: Calculating Taxes
You purchase an item for $60, and the sales tax is 6%. What is the total cost, including tax?
First, calculate the tax amount: Tax = 6% × $60 = 0.06 × $60 = $3.60. Then add the tax to the original price: Total cost = $60 + $3.60 = $63.60.
Example 3: Analyzing Financial Data
A company's profit increased by 15% from the previous year. If the profit last year was $50,000, what is the current profit?
Calculate the increase: Increase = 15% × $50,000 = 0.15 × $50,000 = $7,500. Add the increase to the previous year's profit: Current profit = $50,000 + $7,500 = $57,500.
Example 4: Calculating Interest
You deposit $1000 into a savings account with a 5% annual interest rate. How much interest will you earn after one year?
Interest earned = 5% × $1000 = 0.05 × $1000 = $50.
Advanced Percentage Problems and Solutions
While the problem "16 is 20% of what number?" is relatively straightforward, percentage problems can become more complex. Here are a few examples of more advanced problems and how to approach them:
Example 1: Consecutive Percentage Changes
A price increases by 10% and then decreases by 10%. Is the final price the same as the original price?
No. Consecutive percentage changes do not cancel each other out. Let's illustrate with an example. If the original price is $100:
- 10% increase: $100 + ($100 × 0.10) = $110
- 10% decrease: $110 - ($110 × 0.10) = $99
The final price is $99, which is less than the original price of $100.
Example 2: Finding the Percentage Increase or Decrease
The price of a product increased from $50 to $60. What is the percentage increase?
Percentage increase = [(New Value - Old Value) / Old Value] × 100% = [($60 - $50) / $50] × 100% = (10/50) × 100% = 20%
Example 3: Problems Involving Multiple Percentages
A store offers a 10% discount on an item, and then an additional 5% discount for loyalty members. What is the final price after both discounts?
This problem requires applying the discounts sequentially. Assume the original price is $100:
- 10% discount: $100 - ($100 × 0.10) = $90
- 5% discount (on the discounted price): $90 - ($90 × 0.05) = $85.50
The final price is $85.50.
Tips and Tricks for Solving Percentage Problems
- Convert Percentages to Decimals: This simplifies calculations significantly.
- Use the Formula Consistently: Understanding and applying the basic percentage formula is key.
- Check Your Work: Always verify your answer to ensure accuracy.
- Practice Regularly: The more you practice, the better you'll become at solving percentage problems.
- Use a Calculator: For complex calculations, a calculator can be helpful, but understanding the underlying principles remains crucial.
Conclusion
Solving percentage problems, like determining what number 16 is 20% of, involves understanding the fundamental principles of percentages and applying the appropriate formula or method. This article has provided a detailed explanation of various methods, real-world examples, and advanced problems to enhance your understanding of percentage calculations. By mastering these techniques, you'll be well-equipped to tackle a wide range of percentage-related problems encountered in various fields. Remember, practice is key to building proficiency and confidence in tackling these types of problems.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about 16 Is 20 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.