16 Is 20 Percent Of What Number
News Co
Mar 31, 2025 · 5 min read
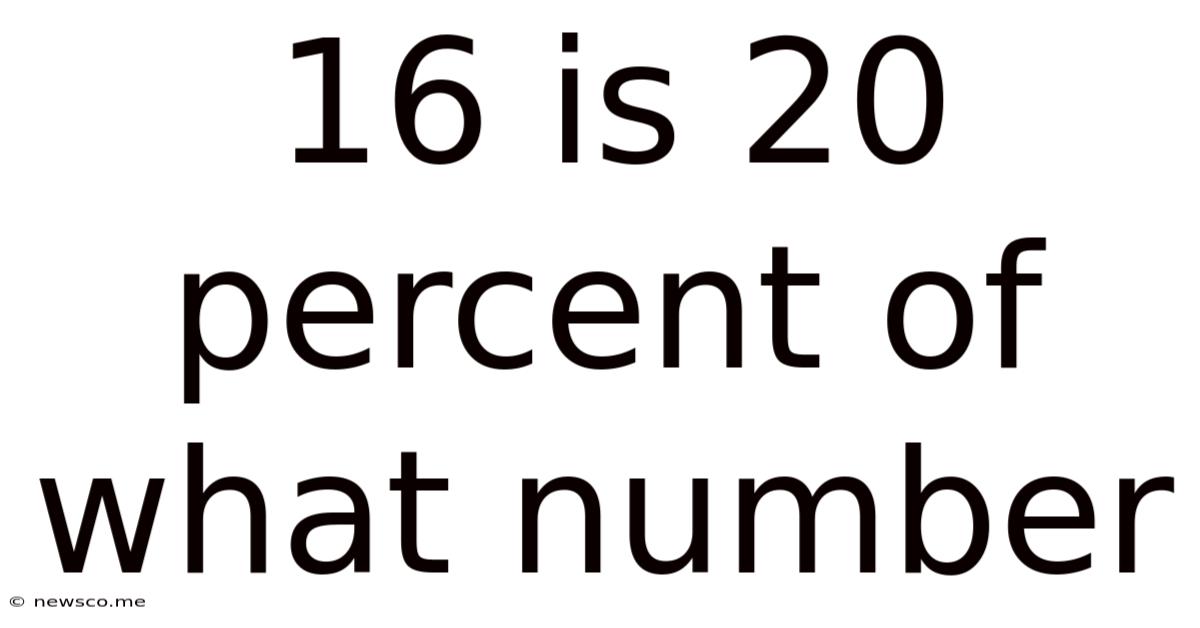
Table of Contents
16 is 20 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Percentage calculations are a fundamental part of everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will delve into the question, "16 is 20 percent of what number?", providing not only the solution but also a detailed explanation of the underlying principles and various methods for solving similar percentage problems. We'll explore different approaches, suitable for various mathematical skill levels, and equip you with the knowledge to confidently tackle percentage calculations in any context.
Understanding the Problem: Deconstructing Percentages
Before diving into the solution, let's dissect the problem statement: "16 is 20 percent of what number?" This seemingly simple sentence encapsulates a crucial relationship between three key elements:
- The Part: This represents a portion of the whole. In our problem, the part is 16.
- The Percentage: This expresses the part as a fraction of the whole, represented as a value out of 100. In this case, the percentage is 20%.
- The Whole: This represents the total quantity from which the part is derived. This is the unknown value we aim to find.
Our goal is to determine the "whole" – the number of which 16 constitutes 20%.
Method 1: Using the Percentage Formula
The most straightforward method to solve this type of problem involves using the standard percentage formula:
Part = (Percentage/100) * Whole
In our case:
- Part = 16
- Percentage = 20
- Whole = x (the unknown value we need to find)
Substituting these values into the formula, we get:
16 = (20/100) * x
Now, we can solve for 'x':
-
Simplify the fraction: 20/100 simplifies to 1/5. The equation becomes: 16 = (1/5) * x
-
Multiply both sides by 5: To isolate 'x', multiply both sides of the equation by 5: 16 * 5 = x
-
Solve for x: 80 = x
Therefore, 16 is 20 percent of 80.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion expresses the equality of two ratios. We can set up a proportion using the given information:
16/x = 20/100
This proportion states that the ratio of the part (16) to the whole (x) is equal to the ratio of the percentage (20) to 100.
To solve for x, we can cross-multiply:
16 * 100 = 20 * x
1600 = 20x
Now, divide both sides by 20:
x = 1600 / 20
x = 80
Again, we find that 16 is 20 percent of 80.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. 20% is equivalent to 0.20 (or simply 0.2). We can rewrite the problem as:
16 = 0.2 * x
To solve for x, divide both sides by 0.2:
x = 16 / 0.2
x = 80
This method reinforces the concept that percentages are simply fractions expressed in hundredths.
Practical Applications: Real-World Scenarios
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item. If the discount amount is $16, you can use the methods above to determine the original price of the item. As we've shown, the original price was $80.
2. Financial Analysis:
In financial statements, percentages are used extensively. For example, if a company reports a 20% increase in profit, and that increase is $16 million, the previous profit can be calculated using the same techniques. The previous profit was $80 million.
3. Statistical Data:
Percentage calculations are essential in interpreting statistical data. For example, if 20% of a survey sample (16 respondents) answered 'yes' to a particular question, the total sample size can be easily determined.
4. Grade Calculations:
If a student scored 16 out of a possible 80 points on a test, and this score represents 20%, it demonstrates a clear understanding of the student's performance relative to the total possible score.
Expanding Your Skills: Solving More Complex Percentage Problems
The principles discussed here can be applied to a broader range of percentage problems. Consider these variations:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, what percentage is 12 of 60? (20%)
-
Finding the part: If you know the whole and the percentage, you can calculate the part. For example, what is 30% of 50? (15)
By mastering these fundamental techniques, you'll develop a strong foundation for tackling more complex percentage calculations. Remember to always carefully identify the "part," "percentage," and "whole" in each problem to set up the equation correctly.
Conclusion: Mastering Percentage Calculations
This in-depth guide has explored multiple methods for solving the problem, "16 is 20 percent of what number?" We've demonstrated how to use the percentage formula, proportions, and decimal equivalents, solidifying the understanding of these core concepts. The practical applications highlighted demonstrate the widespread relevance of percentage calculations in everyday life, from shopping to analyzing financial data. By understanding these fundamental concepts and practicing these methods, you can confidently approach and solve a wide variety of percentage problems, enhancing your mathematical skills and analytical abilities. Remember, the key is to break down the problem, identify the known and unknown variables, and apply the appropriate formula or method to arrive at the correct solution. Practice makes perfect – the more you work with percentage problems, the more intuitive they will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about 16 Is 20 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.