16 Is A Factor Of 8
News Co
Mar 30, 2025 · 5 min read
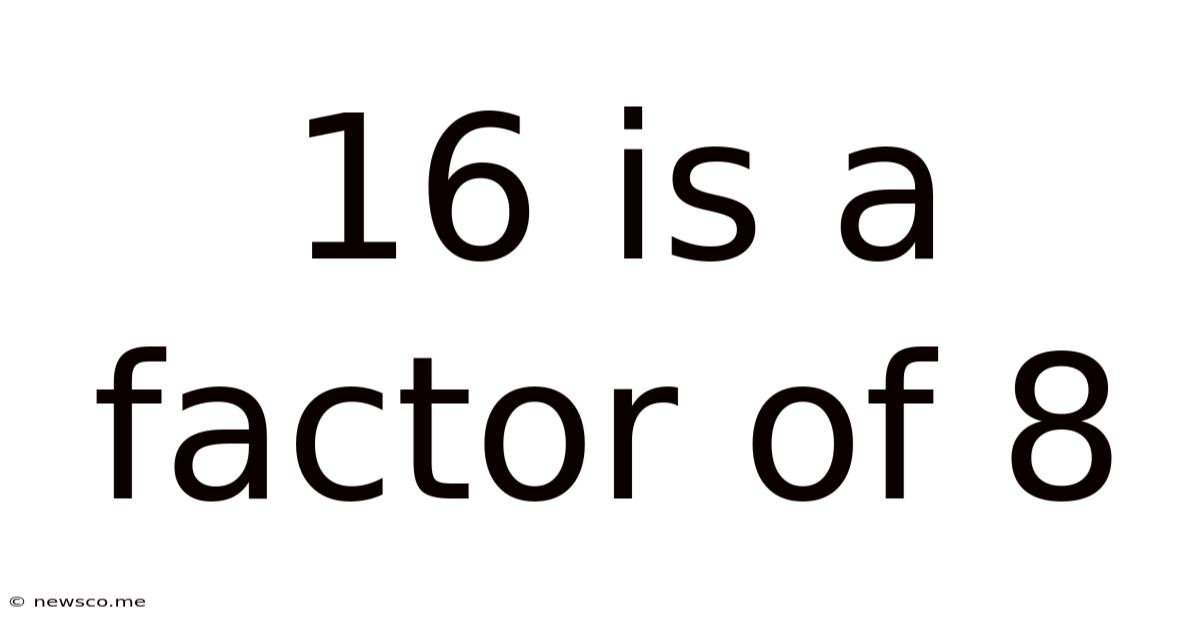
Table of Contents
Is 16 a Factor of 8? Understanding Factors and Divisibility
The statement "16 is a factor of 8" is incorrect. To understand why, we need to delve into the fundamental concepts of factors and divisibility in mathematics. This article will not only explain why 16 isn't a factor of 8 but also explore related concepts, providing a comprehensive understanding of factors, multiples, and divisibility rules. We'll even look at how to effectively approach similar problems and apply these concepts in more advanced mathematical contexts.
What are Factors?
A factor of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number answer, the number you divided by is a factor.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. This is because 12 can be divided evenly by each of these numbers:
- 12 ÷ 1 = 12
- 12 ÷ 2 = 6
- 12 ÷ 3 = 4
- 12 ÷ 4 = 3
- 12 ÷ 6 = 2
- 12 ÷ 12 = 1
Notice that factors always come in pairs. If 'a' is a factor of 'b', then 'b/a' is also a factor of 'b'.
What are Multiples?
A multiple of a number is the result of multiplying that number by any whole number. For instance, the multiples of 3 are 3, 6, 9, 12, 15, and so on.
The relationship between factors and multiples is inverse. If 'a' is a factor of 'b', then 'b' is a multiple of 'a'.
Why 16 is NOT a Factor of 8
Now, let's address the original statement: "16 is a factor of 8". If 16 were a factor of 8, it would mean that 8 divided by 16 would result in a whole number. However, 8 ÷ 16 = 0.5, which is not a whole number. Therefore, 16 is not a factor of 8.
In fact, the factors of 8 are 1, 2, 4, and 8. Since 16 is not on this list, it cannot be a factor of 8. Conversely, 8 is a factor of 16 because 16 ÷ 8 = 2 (a whole number). This highlights the asymmetrical nature of the factor relationship.
Understanding Divisibility Rules
Divisibility rules are shortcuts to determine if a number is divisible by another number without performing the actual division. Knowing these rules can significantly speed up the process of finding factors. Here are some common divisibility rules:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the last two digits are divisible by 4.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 6: A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0.
Applying these rules can help quickly determine if a number is a factor of another. For instance, to check if 16 is a factor of 8, we could try to divide 8 by 16, but observing that 16 is a larger number instantly tells us it's not possible for 16 to be a factor of 8.
Prime Factorization and Factors
Prime factorization is a powerful tool for finding all the factors of a number. A prime number is a whole number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11...). Prime factorization involves expressing a number as a product of its prime factors.
Let's find the prime factorization of 8:
8 = 2 x 4 = 2 x 2 x 2 = 2³
The prime factorization of 8 is 2³. To find all the factors of 8, we consider all possible combinations of these prime factors:
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
- 2³ = 8
Therefore, the factors of 8 are 1, 2, 4, and 8. Again, 16 is not included.
Applying the Concepts to Larger Numbers
Let's consider a more complex example: Is 24 a factor of 72?
First, we perform the division: 72 ÷ 24 = 3. Since the result is a whole number, 24 is a factor of 72.
Alternatively, let's use prime factorization:
- Prime factorization of 24: 2³ x 3
- Prime factorization of 72: 2³ x 3²
Notice that the prime factors of 24 are all contained within the prime factors of 72. This confirms that 24 is a factor of 72.
Common Mistakes and Misconceptions
A common misconception involves confusing factors with multiples. Remembering the inverse relationship between factors and multiples can help avoid this error. If a is a factor of b, then b is a multiple of a. It is not possible for a number to simultaneously be a factor and a multiple of itself, except for 1, and numbers greater than 1 always have factors which are less than the number itself.
Another mistake is assuming that larger numbers are always factors of smaller numbers. The size of a number has no bearing on whether it's a factor of another number. Always perform the division or use prime factorization to determine if one number is a factor of another.
Conclusion: Factors and Divisibility in Real-World Applications
Understanding factors and divisibility is crucial not just in pure mathematics, but also in various practical applications. From dividing resources equally to determining the dimensions of objects or optimizing computer algorithms, the concept of factors plays a significant role. Mastering the techniques discussed in this article – understanding divisibility rules, using prime factorization, and recognizing the relationship between factors and multiples – provides a solid foundation for solving various mathematical problems and for understanding a range of mathematical concepts. By correctly identifying factors and understanding the principles of divisibility, we can effectively approach a wide array of computational and mathematical challenges. It's a foundational skill that extends far beyond the classroom, proving essential in numerous fields of study and real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 16 Is A Factor Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.