16 Is What Percent Of 25
News Co
Apr 13, 2025 · 4 min read
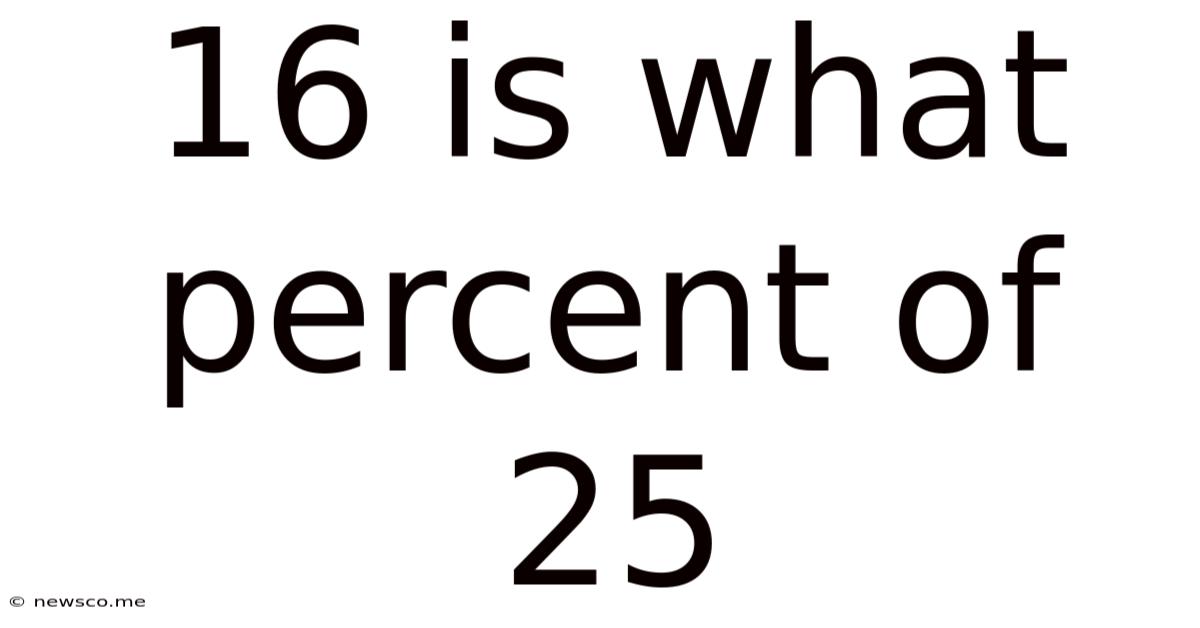
Table of Contents
16 is What Percent of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article delves into the seemingly simple question, "16 is what percent of 25?", providing a comprehensive explanation, practical examples, and advanced techniques to master percentage calculations. We'll explore various methods, highlighting their advantages and applications, ensuring you gain a solid grasp of this crucial concept.
Understanding Percentages: The Basics
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Key Terms and Concepts
- Percent: A ratio expressed as a fraction of 100.
- Base: The original number or whole amount (in our case, 25).
- Part: The portion of the base (in our case, 16).
- Rate: The percentage that represents the relationship between the part and the base (what we need to find).
Method 1: Using the Percentage Formula
The most straightforward method to solve "16 is what percent of 25?" is employing the basic percentage formula:
(Part / Base) x 100% = Rate
Let's substitute the values:
(16 / 25) x 100% = Rate
Performing the calculation:
0.64 x 100% = 64%
Therefore, 16 is 64% of 25.
Real-World Application: Discount Calculation
Imagine a shirt originally priced at $25 is on sale for $16. Using the percentage formula, we've determined the discount is 64%. This calculation is vital for understanding savings and making informed purchasing decisions.
Method 2: Proportion Method
Another effective approach uses proportions. We can set up a proportion to solve for the unknown percentage:
16/25 = x/100
Where 'x' represents the percentage we're trying to find. To solve this proportion, we cross-multiply:
16 * 100 = 25 * x
1600 = 25x
x = 1600 / 25
x = 64
Thus, 16 is 64% of 25.
Real-World Application: Survey Results
Suppose a survey of 25 people revealed that 16 preferred a particular brand. Using the proportion method, we easily calculate that 64% of respondents favored that brand. This method is frequently used in data analysis and statistical reporting.
Method 3: Using Decimals
Converting the fraction to a decimal provides another path to the solution:
16/25 = 0.64
To express this decimal as a percentage, we multiply by 100%:
0.64 x 100% = 64%
Again, we arrive at the conclusion that 16 is 64% of 25.
Real-World Application: Grade Calculation
If you scored 16 out of 25 on a test, converting the fraction to a decimal (0.64) and then to a percentage (64%) gives you your percentage grade. This method is particularly useful for quickly assessing performance in various academic or professional settings.
Advanced Percentage Calculations and Applications
While the problem "16 is what percent of 25?" is relatively simple, understanding the underlying principles allows you to tackle more complex percentage calculations. Let's explore some advanced applications:
Finding the Base
Sometimes, you might know the percentage and the part, but need to find the base. For example: "16 is 64% of what number?" The formula becomes:
Base = (Part / Rate) x 100
In this case:
Base = (16 / 64%) x 100 = 25
Finding the Part
Conversely, you may know the percentage and the base, but need to find the part. For example: "What is 64% of 25?" The formula is:
Part = (Rate / 100) x Base
In this case:
Part = (64 / 100) x 25 = 16
Percentage Increase and Decrease
Calculating percentage changes is crucial in various contexts. The formula for percentage increase is:
[(New Value - Original Value) / Original Value] x 100%
For a percentage decrease, the formula is:
[(Original Value - New Value) / Original Value] x 100%
For instance, if a product's price increases from $25 to $30, the percentage increase is:
[(30 - 25) / 25] x 100% = 20%
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering any mathematical concept. Work through various problems, gradually increasing their complexity.
- Use Different Methods: Familiarize yourself with multiple methods (formula, proportion, decimals). Choosing the most suitable method will depend on the specific problem and your comfort level.
- Check Your Work: Always double-check your calculations to avoid errors. Use a calculator if necessary to ensure accuracy.
- Visual Aids: Utilize visual aids like diagrams or charts to help visualize the relationships between the part, base, and rate.
Conclusion: Beyond the Basics of Percentages
The seemingly simple question, "16 is what percent of 25?", serves as a gateway to a broader understanding of percentages. By mastering the fundamental methods and exploring advanced applications, you equip yourself with a valuable skill applicable to diverse real-world situations. From personal finance and shopping to scientific research and data analysis, the ability to calculate and interpret percentages is indispensable for informed decision-making and effective problem-solving. Remember that consistent practice and the exploration of different calculation methods are the key to unlocking your full potential in working with percentages.
Latest Posts
Related Post
Thank you for visiting our website which covers about 16 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.