16 To The Power Of 1/4
News Co
Mar 21, 2025 · 5 min read
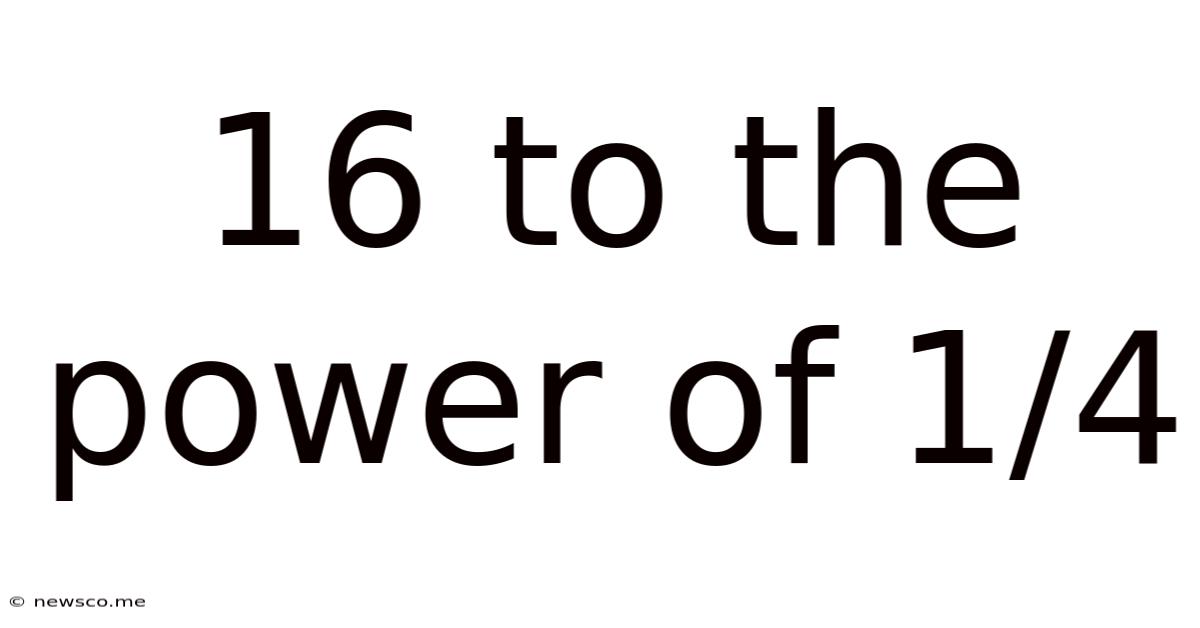
Table of Contents
16 to the Power of 1/4: A Deep Dive into Fractional Exponents
Understanding fractional exponents can seem daunting at first, but they're a fundamental concept in mathematics with wide-ranging applications in various fields. This article provides a comprehensive exploration of 16 to the power of 1/4 (16<sup>1/4</sup>), delving into the meaning of fractional exponents, the methods for calculating them, and their significance in different mathematical contexts. We'll also touch upon real-world applications and explore some related concepts to solidify your understanding.
What Does 16<sup>1/4</sup> Mean?
Before tackling the calculation, let's clarify what 16<sup>1/4</sup> actually represents. The exponent 1/4 signifies the fourth root. In simpler terms, we're looking for a number that, when multiplied by itself four times, equals 16. This is directly related to the concept of roots and radicals.
Understanding Roots and Radicals:
The expression 16<sup>1/4</sup> is equivalent to the fourth root of 16, often written as <sup>4</sup>√16. The number 4 is called the index, indicating the root we're seeking. The number 16 is the radicand, the number under the radical symbol (√).
Connecting Exponents and Roots:
The relationship between exponents and roots is crucial. The fractional exponent a<sup>m/n</sup> is equivalent to the nth root of a raised to the power of m. In our case, 16<sup>1/4</sup> can be expressed as (16<sup>1</sup>)<sup>1/4</sup> or <sup>4</sup>√16<sup>1</sup>, simplifying to just <sup>4</sup>√16.
Calculating 16<sup>1/4</sup>
Now, let's determine the value of 16<sup>1/4</sup>. We are looking for a number that, when multiplied by itself four times, results in 16. Through simple trial and error, or a more methodical approach, we can find the answer:
-
Method 1: Trial and Error: Let's test some numbers. 2 x 2 x 2 x 2 = 16. Therefore, 16<sup>1/4</sup> = 2.
-
Method 2: Prime Factorization: We can break down 16 into its prime factors. 16 = 2 x 2 x 2 x 2 = 2<sup>4</sup>. Substituting this into our original expression, we get (2<sup>4</sup>)<sup>1/4</sup>. Using the rule of exponents (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>, we simplify this to 2<sup>(4)(1/4)</sup> = 2<sup>1</sup> = 2.
Therefore, both methods confirm that 16<sup>1/4</sup> = 2.
Extending the Concept: Fractional Exponents with Numerators Other Than 1
While 16<sup>1/4</sup> illustrates a fractional exponent with a numerator of 1, the concept extends to fractional exponents with any integer numerator. Consider a more general case: a<sup>m/n</sup>.
Recall that a<sup>m/n</sup> = (a<sup>1/n</sup>)<sup>m</sup> = (<sup>n</sup>√a)<sup>m</sup>. This means we first take the nth root of a and then raise the result to the power of m.
Example: Calculate 8<sup>2/3</sup>.
Using the rule above, 8<sup>2/3</sup> = (8<sup>1/3</sup>)<sup>2</sup>.
- Find the cube root of 8: 8<sup>1/3</sup> = 2 (since 2 x 2 x 2 = 8)
- Raise the result to the power of 2: 2<sup>2</sup> = 4
Therefore, 8<sup>2/3</sup> = 4.
Negative Fractional Exponents
The concept also extends to negative fractional exponents. Remember that a<sup>-m/n</sup> = 1/(a<sup>m/n</sup>). This means a negative fractional exponent represents the reciprocal of the corresponding positive fractional exponent.
Example: Calculate 16<sup>-1/4</sup>.
Since 16<sup>1/4</sup> = 2, then 16<sup>-1/4</sup> = 1/16<sup>1/4</sup> = 1/2 = 0.5.
Applications of Fractional Exponents
Fractional exponents are not just abstract mathematical concepts; they have practical applications across diverse fields:
1. Geometry and Measurement:
Calculating volumes, areas, and lengths often involves fractional exponents. For instance, finding the side length of a cube given its volume requires using a cube root (exponent of 1/3).
2. Physics and Engineering:
Many physical phenomena, such as wave propagation, radioactive decay, and the behavior of springs, are modeled using equations involving fractional exponents.
3. Finance and Economics:
Compound interest calculations rely on fractional exponents to determine the growth of investments over time. The concept is also integral to understanding various financial models and economic growth projections.
4. Computer Science and Programming:
Algorithms and data structures often use fractional exponents for operations like root finding and optimization.
5. Statistics and Data Analysis:
Fractional exponents are used in statistical distributions and modelling various datasets and probabilities.
Advanced Concepts and Further Exploration
This section will explore some related mathematical concepts to further enhance your understanding of fractional exponents.
1. Complex Numbers and Fractional Exponents:
The concept of fractional exponents can be extended to complex numbers, leading to more intricate calculations and applications in advanced mathematics and physics.
2. Irrational Exponents:
While we've focused on rational exponents (fractions), the concept extends to irrational exponents (like π or √2). These calculations often require advanced mathematical techniques.
3. Logarithms and their Relationship to Exponents:
Logarithms are the inverse of exponential functions. Understanding logarithms provides an alternative approach to solving problems involving exponents, including fractional exponents.
4. Newton's Method for Approximating Roots:
For situations where finding the exact root is difficult, numerical methods like Newton's method can provide accurate approximations of fractional exponents.
Conclusion: Mastering Fractional Exponents
Understanding 16<sup>1/4</sup> and the broader concept of fractional exponents is crucial for anyone pursuing studies in mathematics, science, engineering, or related fields. By mastering these concepts and their related calculations, you equip yourself with powerful tools applicable across various domains. This article served as a comprehensive guide, covering the fundamentals, calculation methods, applications, and related concepts, enabling you to confidently tackle more complex problems involving fractional exponents. Remember to practice regularly to solidify your understanding and unlock the potential of this fundamental mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 16 To The Power Of 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.