17 15 As A Mixed Number
News Co
May 08, 2025 · 5 min read
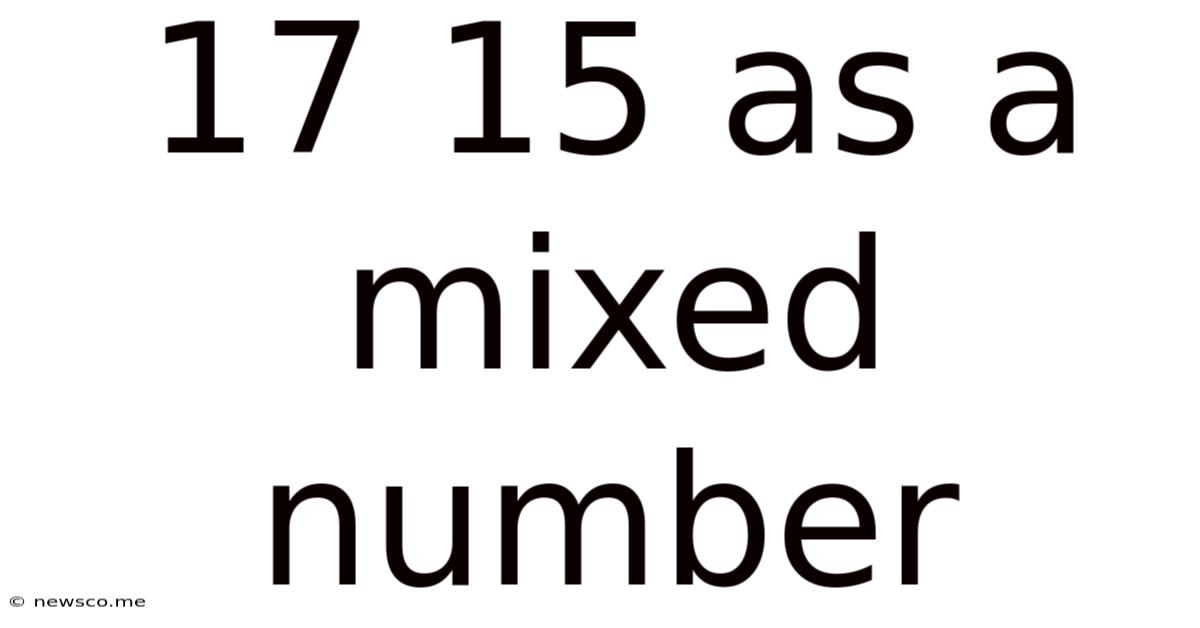
Table of Contents
17/15 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 17/15, into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 17/15 into a mixed number but will also delve into the underlying concepts, provide alternative methods, and explore practical applications. We’ll also touch upon related topics to solidify your understanding of fractions and mixed numbers.
Understanding Fractions and Mixed Numbers
Before we dive into the conversion of 17/15, let's refresh our understanding of fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
Improper Fractions: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 17/15, 5/4, 8/8).
Mixed Numbers: A mixed number combines a whole number and a proper fraction (e.g., 1 2/3, 2 1/4, 3 3/8). A proper fraction has a numerator smaller than the denominator.
Converting 17/15 to a Mixed Number: The Standard Method
The most common method for converting an improper fraction to a mixed number involves division.
-
Divide the numerator by the denominator: Divide 17 by 15. 17 ÷ 15 = 1 with a remainder of 2.
-
The quotient becomes the whole number part: The quotient (1) is the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction part: The remainder (2) becomes the numerator of the fraction.
-
The denominator remains the same: The denominator (15) stays the same.
Therefore, 17/15 as a mixed number is 1 2/15.
Visualizing the Conversion
Imagine you have 17 slices of pizza, and each pizza has 15 slices. You can make one whole pizza (15 slices) and have 2 slices left over. This represents 1 whole pizza and 2/15 of another pizza – hence, 1 2/15.
Alternative Methods for Conversion
While the standard division method is straightforward, there are alternative approaches you can use, especially for mental calculations or to deepen your understanding.
Method 2: Subtracting the denominator repeatedly:
- Start with the improper fraction 17/15.
- Subtract the denominator (15) from the numerator (17): 17 - 15 = 2.
- The number of times you subtracted the denominator (once) becomes the whole number.
- The remainder (2) becomes the numerator of the fraction, and the denominator remains the same (15).
- This gives us the mixed number: 1 2/15.
This method is particularly helpful for visualizing the process and understanding the concept behind the conversion.
Converting Mixed Numbers back to Improper Fractions
It's equally important to be able to convert a mixed number back into an improper fraction. Let's convert 1 2/15 back to an improper fraction:
- Multiply the whole number by the denominator: 1 * 15 = 15.
- Add the numerator to the result: 15 + 2 = 17.
- Keep the denominator the same: The denominator remains 15.
Therefore, 1 2/15 converts back to the improper fraction 17/15.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in various real-life situations:
- Measurement: Expressing measurements like 2 1/2 inches or 3 3/4 cups.
- Cooking/Baking: Following recipes that require specific quantities of ingredients.
- Construction: Calculating dimensions and material requirements.
- Time: Representing time intervals like 1 hour and 30 minutes (1 1/2 hours).
Understanding how to work with mixed numbers is crucial for accurate calculations and problem-solving in these and many other contexts.
Simplifying Fractions (A Crucial Step)
Before representing a fraction as a mixed number or vice-versa, it is essential to always simplify the fraction to its lowest terms. This makes calculations easier and ensures the most accurate representation. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1.
In the case of 17/15, the GCD of 17 and 15 is 1, meaning the fraction is already in its simplest form. However, if we had a fraction like 18/12, we would simplify it first:
The GCD of 18 and 12 is 6. Dividing both the numerator and the denominator by 6, we get 3/2. Now, we convert 3/2 to a mixed number: 1 1/2.
Working with Larger Numbers
The principles remain the same even when dealing with larger numbers. For example, let's convert 47/8 to a mixed number:
- Divide 47 by 8: 47 ÷ 8 = 5 with a remainder of 7.
- The whole number is 5.
- The remainder is 7, and the denominator remains 8.
- Therefore, 47/8 = 5 7/8.
Error Handling and Common Mistakes
When converting improper fractions to mixed numbers, some common errors can occur:
- Incorrect division: Double-check your division to ensure accuracy.
- Forgetting the remainder: Remember that the remainder becomes the numerator of the fraction part.
- Incorrect simplification: Always simplify the fraction part to its lowest terms.
Beyond the Basics: Extending Your Knowledge
Understanding mixed numbers is a foundational step towards more advanced mathematical concepts. From here, you can explore:
- Adding and subtracting mixed numbers: This involves converting to improper fractions for easier calculation, then converting back to mixed numbers.
- Multiplying and dividing mixed numbers: Similar to addition and subtraction, it often simplifies the process to convert to improper fractions first.
- Working with mixed numbers in algebraic equations: Mixed numbers can be integrated into various algebraic expressions and equations.
Mastering the conversion between improper fractions and mixed numbers is a fundamental step in your mathematical journey, opening doors to more complex problem-solving and a deeper understanding of numbers. Remember to practice regularly, and don't hesitate to explore different methods to find the approach that best suits your learning style. With consistent practice and a clear understanding of the underlying principles, you'll be confident in handling mixed numbers in any situation.
Latest Posts
Latest Posts
-
What Is The Csc Of 0
May 08, 2025
-
How To Write 1250 00 On A Check
May 08, 2025
-
All Real Numbers Are Rational True Or False
May 08, 2025
-
0 33 As A Fraction In Simplest Form
May 08, 2025
-
How Many Weeks Until April 1
May 08, 2025
Related Post
Thank you for visiting our website which covers about 17 15 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.