17 5 As A Mixed Number
News Co
Mar 19, 2025 · 5 min read
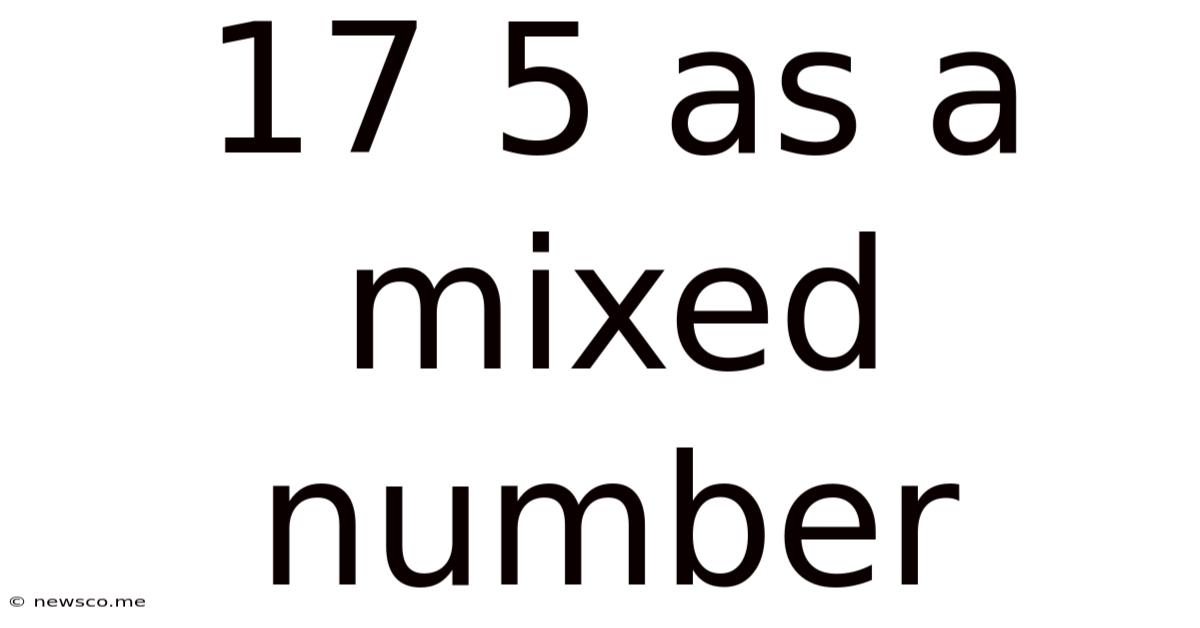
Table of Contents
17/5 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 17/5 into a mixed number, explaining the underlying concepts and providing practical examples. We'll also explore related concepts to solidify your understanding.
Understanding Improper Fractions and Mixed Numbers
Before we dive into converting 17/5, let's clarify the definitions of improper fractions and mixed numbers.
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For instance, 17/5 is an improper fraction because 17 (numerator) is greater than 5 (denominator).
Mixed Number: A mixed number is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator. For example, 3 2/5 is a mixed number; it represents three whole units and two-fifths of another unit.
Converting 17/5 to a Mixed Number: Step-by-Step
The conversion of 17/5 to a mixed number involves dividing the numerator by the denominator. Here's a detailed breakdown:
-
Divide the Numerator by the Denominator: Divide 17 by 5. This gives us a quotient of 3 and a remainder of 2.
-
Identify the Whole Number: The quotient (3) becomes the whole number part of the mixed number.
-
Form the Proper Fraction: The remainder (2) becomes the numerator of the proper fraction, and the original denominator (5) remains the denominator. This gives us the fraction 2/5.
-
Combine the Whole Number and Proper Fraction: Combine the whole number (3) and the proper fraction (2/5) to form the mixed number: 3 2/5.
Therefore, 17/5 expressed as a mixed number is 3 2/5.
Visual Representation of 17/5
Imagine you have 17 identical objects. If you want to group them into sets of 5, you can form three complete sets (3 x 5 = 15), with 2 objects remaining (17 - 15 = 2). This visually demonstrates that 17/5 equals 3 whole sets and 2/5 of another set – hence, 3 2/5.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields:
-
Cooking and Baking: Recipes often call for mixed numbers of ingredients, such as 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder.
-
Measurement: Measuring length, weight, or volume frequently involves mixed numbers. For example, a board might measure 4 3/8 feet long.
-
Construction: Construction projects rely heavily on precise measurements, often expressed using mixed numbers.
-
Engineering: Engineers use mixed numbers in calculations related to dimensions, quantities, and ratios.
Converting Mixed Numbers Back to Improper Fractions
It's also essential to understand the reverse process: converting a mixed number back into an improper fraction. Let's convert 3 2/5 back to an improper fraction:
-
Multiply the whole number by the denominator: 3 x 5 = 15
-
Add the numerator: 15 + 2 = 17
-
Keep the same denominator: The denominator remains 5.
-
Form the improper fraction: The result is 17/5.
This demonstrates the equivalence between the mixed number 3 2/5 and the improper fraction 17/5.
Other Examples of Converting Improper Fractions to Mixed Numbers
Let's explore a few more examples to reinforce the concept:
-
22/7: Dividing 22 by 7 gives a quotient of 3 and a remainder of 1. Therefore, 22/7 = 3 1/7.
-
35/8: Dividing 35 by 8 gives a quotient of 4 and a remainder of 3. Therefore, 35/8 = 4 3/8.
-
100/12: Dividing 100 by 12 gives a quotient of 8 and a remainder of 4. Therefore, 100/12 = 8 4/12. Note that this fraction can be simplified to 8 1/3 by dividing both the numerator and denominator by 4.
Simplifying Fractions: A Crucial Step
Often, after converting an improper fraction to a mixed number, the resulting proper fraction can be simplified. Simplification involves dividing both the numerator and denominator by their greatest common divisor (GCD). For instance, in the example of 100/12 converted to 8 4/12, the fraction 4/12 can be simplified to 1/3 by dividing both the numerator (4) and the denominator (12) by their GCD, which is 4.
Finding the GCD: There are several methods for finding the greatest common divisor, including listing factors or using the Euclidean algorithm. For smaller numbers, listing factors is often the easiest approach.
Importance of Mastering Fraction Conversion
The ability to confidently convert between improper fractions and mixed numbers is crucial for success in mathematics and related fields. It's a fundamental building block for more advanced mathematical concepts, including algebraic manipulation, calculus, and more. A strong grasp of fractions is essential for accurate calculations and problem-solving in various real-world scenarios.
Tips for Success in Fraction Conversion
-
Practice regularly: The more you practice, the more comfortable and proficient you will become in converting fractions.
-
Use visual aids: Diagrams and other visual representations can help solidify your understanding of the concept.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Seek help when needed: Don't hesitate to ask for assistance from teachers, tutors, or classmates if you encounter difficulties.
Conclusion: Mastering the Art of Fraction Conversion
Converting 17/5 to the mixed number 3 2/5 is a straightforward process once you understand the underlying principles. This guide has provided a comprehensive explanation of the steps involved, practical applications, and related concepts, equipping you with the knowledge and skills to confidently convert any improper fraction into its equivalent mixed number form and vice-versa. Remember, consistent practice is key to mastering this fundamental mathematical skill. By understanding the relationship between improper fractions and mixed numbers, you'll improve your overall mathematical proficiency and open doors to more advanced mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 17 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.