18 Of What Number Is 90
News Co
May 08, 2025 · 5 min read
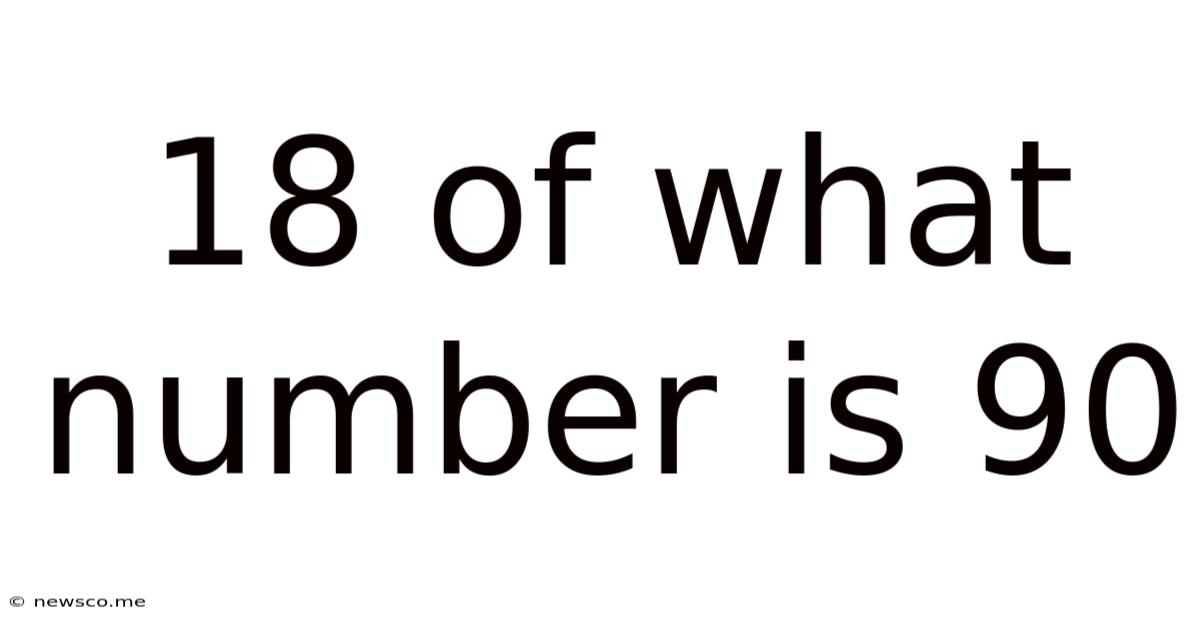
Table of Contents
18 of What Number is 90? Unlocking the Power of Percentage Calculations
This seemingly simple question, "18 of what number is 90?", opens the door to a fascinating world of percentage calculations. Understanding how to solve this, and similar problems, is crucial for everyday life, from calculating discounts and taxes to understanding financial reports and even mastering more complex mathematical concepts. This article will delve deep into the solution, exploring different methods, and explaining the underlying principles. We'll also explore the broader application of percentage calculations, providing you with a robust understanding of this essential mathematical skill.
Understanding the Problem: Deconstructing "18 of What Number is 90?"
Before diving into the solution, let's break down the question itself. The phrase "18 of what number is 90" implies a relationship between three key elements:
- 18: This represents a part or percentage of a larger whole.
- 90: This is the known value of that part.
- The Unknown Number: This is the whole number we need to find. This is the core of the problem.
Essentially, we're trying to determine what number, when multiplied by 18/100 (or 0.18), will result in 90.
Method 1: Using Algebra to Solve for the Unknown
Algebra provides a powerful and straightforward method for solving this problem. We can represent the unknown number with a variable, such as 'x'. The problem can then be expressed as an equation:
0.18x = 90
To solve for 'x', we need to isolate it on one side of the equation. We can do this by dividing both sides by 0.18:
x = 90 / 0.18
Performing the division, we get:
x = 500
Therefore, 18% of 500 is 90.
Method 2: Setting up a Proportion
Proportions offer another effective approach. We can set up a proportion where one ratio represents the known part (18) to the whole (unknown, represented by 'x'), and the other ratio represents the known value of that part (90) to the total (100%). This gives us:
18/x = 90/100
To solve this proportion, we can cross-multiply:
18 * 100 = 90 * x
1800 = 90x
Now, divide both sides by 90:
x = 1800 / 90
x = 500
Again, we find that the unknown number is 500.
Method 3: Using Percentage Calculation Formula
The percentage calculation formula offers a more direct approach. The formula is:
(Part / Whole) * 100% = Percentage
In our case, we know the part (90) and the percentage (18%). We need to find the whole. Rearranging the formula to solve for the whole, we get:
Whole = (Part / Percentage) * 100
Substituting our values:
Whole = (90 / 18) * 100
Whole = 5 * 100
Whole = 500
Verifying the Solution
It's always good practice to verify your solution. Let's check if 18% of 500 is indeed 90:
(18/100) * 500 = 90
The calculation confirms our solution.
Expanding the Understanding: Percentage Calculations in Real-World Scenarios
Understanding percentage calculations is crucial for navigating numerous real-world situations. Here are a few examples:
1. Calculating Discounts:
Imagine a store offers a 20% discount on a $150 item. To calculate the discount amount, you'd use the formula:
Discount Amount = (Discount Percentage / 100) * Original Price
Discount Amount = (20 / 100) * $150 = $30
The final price would be $150 - $30 = $120.
2. Determining Tax Amounts:
Suppose a sales tax is 6%. To calculate the tax on a $200 purchase, you would use the same principle:
Tax Amount = (Tax Percentage / 100) * Purchase Price
Tax Amount = (6 / 100) * $200 = $12
The total cost, including tax, would be $200 + $12 = $212.
3. Analyzing Financial Statements:
Percentage calculations are essential for interpreting financial statements. For example, understanding profit margins (profit as a percentage of revenue), debt-to-equity ratios, and return on investment (ROI) all rely heavily on percentage calculations.
4. Understanding Statistics and Data Analysis:
Percentages are fundamental in statistics. Representing data as percentages makes it easier to compare and interpret different datasets. For example, understanding the percentage of a population holding a specific viewpoint, or the percentage change in a particular metric over time.
5. Everyday Problem Solving:
Even seemingly simple everyday tasks can benefit from an understanding of percentages. For example, calculating tips in restaurants, determining the percentage of a task completed, or figuring out the best deal when comparing prices.
Beyond the Basics: More Complex Percentage Problems
While the initial problem was straightforward, percentage calculations can become more complex. Here are some examples:
-
Calculating percentage increase or decrease: This involves determining the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%.
-
Finding the original value after a percentage increase or decrease: This requires working backwards from the final value to find the original value. This often involves using algebra to solve for the unknown.
-
Compound interest calculations: This involves calculating interest on both the principal amount and accumulated interest over time. This requires more advanced mathematical concepts.
-
Working with multiple percentages: Situations often arise where you need to work with multiple percentage changes, requiring careful sequencing of calculations.
Mastering Percentage Calculations: Tips and Resources
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying principles. Here are some tips:
-
Practice regularly: Solve various problems, starting with simple ones and gradually increasing the difficulty.
-
Understand the underlying concepts: Don't just memorize formulas; understand why they work.
-
Use different methods: Experiment with various approaches (algebra, proportions, formula) to find the methods that suit your learning style best.
-
Verify your solutions: Always double-check your answers to ensure accuracy.
-
Utilize online resources: Many websites and educational platforms offer practice problems, tutorials, and explanations on percentage calculations.
By mastering percentage calculations, you equip yourself with a powerful tool applicable across various fields, making it easier to navigate the complexities of everyday life and professional endeavors. The seemingly simple question of "18 of what number is 90?" has opened up a world of possibilities. The key is consistent practice and a willingness to delve deeper into the underlying mathematical principles.
Latest Posts
Latest Posts
-
What Is A Triangle With 2 Equal Sides
May 08, 2025
-
What Is The Absolute Value Of 10
May 08, 2025
-
Adding Subtracting Multiplying Dividing Fractions Worksheet
May 08, 2025
-
What Is The Prime Factorization Of 375
May 08, 2025
-
How Do You Find The Perimeter Of An Octagon
May 08, 2025
Related Post
Thank you for visiting our website which covers about 18 Of What Number Is 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.