2 1 4 Percent As A Decimal
News Co
Mar 29, 2025 · 5 min read
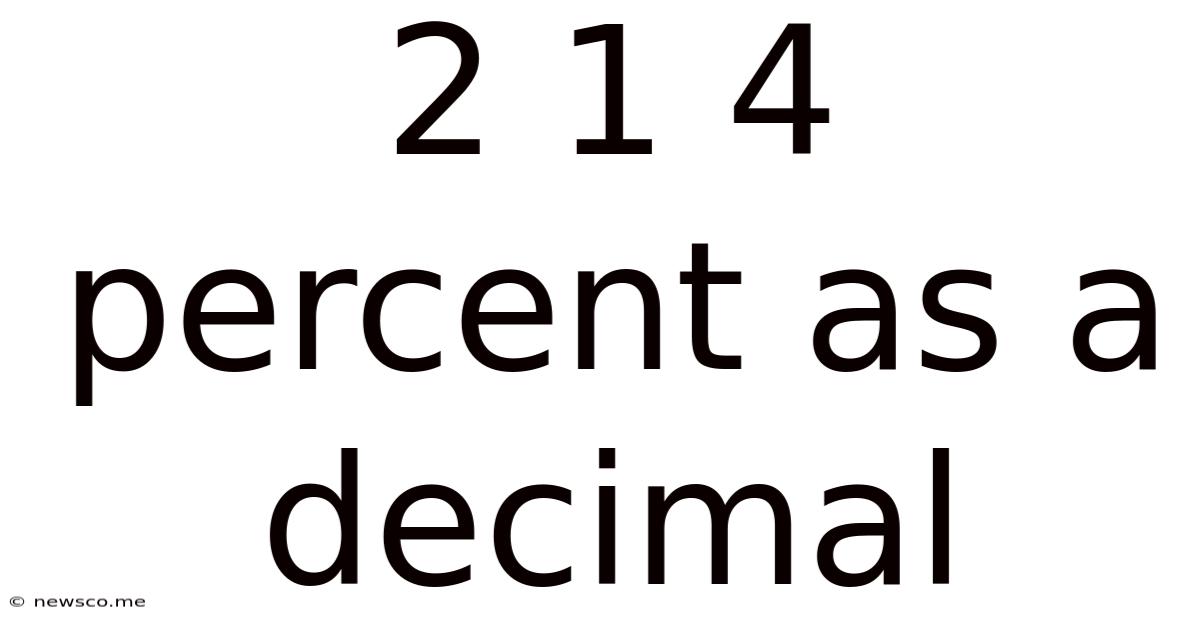
Table of Contents
- 2 1 4 Percent As A Decimal
- Table of Contents
- 2 1/4 Percent as a Decimal: A Comprehensive Guide
- Understanding Percentages and Decimals
- Converting 2 1/4 Percent to a Decimal: A Step-by-Step Approach
- Practical Applications of Decimal Conversions
- Related Concepts and Further Exploration
- Advanced Examples and Practice Problems
- Latest Posts
- Related Post
2 1/4 Percent as a Decimal: A Comprehensive Guide
Converting fractions and percentages to decimals is a fundamental skill in mathematics with applications across numerous fields, from finance and accounting to engineering and data science. This comprehensive guide will meticulously explore the conversion of 2 1/4 percent to its decimal equivalent, explaining the process step-by-step and providing additional examples to solidify your understanding. We'll also delve into the practical applications of this conversion and explore related concepts.
Understanding Percentages and Decimals
Before we tackle the conversion, let's establish a clear understanding of percentages and decimals.
What is a Percentage?
A percentage represents a fraction of 100. The symbol "%" signifies "per hundred." For instance, 50% means 50 out of 100, or 50/100. This can be simplified to 1/2 or 0.5.
What is a Decimal?
A decimal is a way of writing a number that is not a whole number. It uses a decimal point (.) to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of powers of 10 (tenths, hundredths, thousandths, and so on). For example, 0.5 represents five-tenths, and 0.75 represents seventy-five hundredths.
Converting 2 1/4 Percent to a Decimal: A Step-by-Step Approach
The conversion of 2 1/4% to a decimal involves several key steps:
Step 1: Convert the Mixed Fraction to an Improper Fraction
The first step is to convert the mixed fraction 2 1/4 into an improper fraction. To do this, we multiply the whole number (2) by the denominator (4), add the numerator (1), and keep the same denominator:
(2 * 4) + 1 = 9
Therefore, 2 1/4 becomes 9/4.
Step 2: Convert the Percentage to a Fraction
Now, we have 9/4 percent. Remember that "percent" means "per hundred," so we can express this as a fraction:
9/4% = 9/4 / 100
Step 3: Simplify the Complex Fraction
We now have a complex fraction (a fraction within a fraction). To simplify, we multiply the numerator by the reciprocal of the denominator:
(9/4) * (1/100) = 9/400
Step 4: Convert the Fraction to a Decimal
Finally, we convert the fraction 9/400 to a decimal by performing the division:
9 ÷ 400 = 0.0225
Therefore, 2 1/4% as a decimal is 0.0225.
Practical Applications of Decimal Conversions
The ability to convert between percentages, fractions, and decimals is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, and tax amounts often involves converting between these forms. For example, understanding that a 2.25% interest rate is equivalent to 0.0225 allows for easier calculations in compound interest formulas.
-
Data Analysis: In statistics and data analysis, representing data in decimal form is often more convenient for calculations and analysis. Converting percentages to decimals is essential for working with statistical software and interpreting results.
-
Engineering: In engineering design and calculations, precise measurements are critical. Converting fractions and percentages to decimals ensures accuracy in calculations involving dimensions, tolerances, and other critical parameters.
-
Everyday Life: Many everyday situations involve percentage calculations, such as calculating tips, sales discounts, or the percentage of a task completed. Understanding the decimal equivalent can simplify these computations.
Related Concepts and Further Exploration
Understanding the conversion of 2 1/4% to a decimal lays a foundation for exploring several related mathematical concepts:
1. Decimal Place Value: Gaining a deeper understanding of decimal place value (tenths, hundredths, thousandths, etc.) is crucial for accurately representing and manipulating decimal numbers.
2. Significant Figures: When dealing with decimal numbers resulting from measurements or calculations, understanding significant figures helps determine the accuracy and precision of the result.
3. Rounding Decimals: Often, you'll need to round decimal numbers to a certain number of decimal places to simplify the result or adhere to specific precision requirements.
4. Percentage Increase/Decrease: Calculating percentage increase or decrease is a common application of decimal conversions, involving adding or subtracting the decimal equivalent of the percentage change from the original value.
5. Converting Decimals to Fractions and Percentages: The reverse conversions (decimal to fraction, decimal to percentage) are equally important and should be mastered for comprehensive understanding.
Advanced Examples and Practice Problems
Let's explore some additional examples to further solidify your understanding of converting percentages to decimals:
Example 1: Converting 3 3/8% to a decimal
- Convert the mixed fraction 3 3/8 to an improper fraction: (3 * 8) + 3 = 27/8
- Convert the percentage to a fraction: 27/8 / 100 = 27/800
- Convert the fraction to a decimal: 27 ÷ 800 = 0.03375
Therefore, 3 3/8% is equal to 0.03375 as a decimal.
Example 2: Converting 1/8% to a decimal
- Convert the fraction to a decimal: 1 ÷ 8 = 0.125
- Convert the percentage to a decimal: 0.125 / 100 = 0.00125
Therefore, 1/8% is equal to 0.00125 as a decimal.
Practice Problems:
Try converting the following percentages to decimals:
- 5 1/2%
- 1/4%
- 12 1/4%
- 7/8%
- 25 3/4%
By working through these examples and practice problems, you'll build confidence and proficiency in converting percentages to decimals. Remember that consistent practice is key to mastering this essential mathematical skill. Understanding the underlying concepts and applying them systematically will make the conversion process straightforward and efficient. The ability to confidently convert between percentages, fractions, and decimals opens doors to solving a wide array of practical problems across various disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 1 4 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.