2 3 2 3 2 3
News Co
Mar 30, 2025 · 5 min read
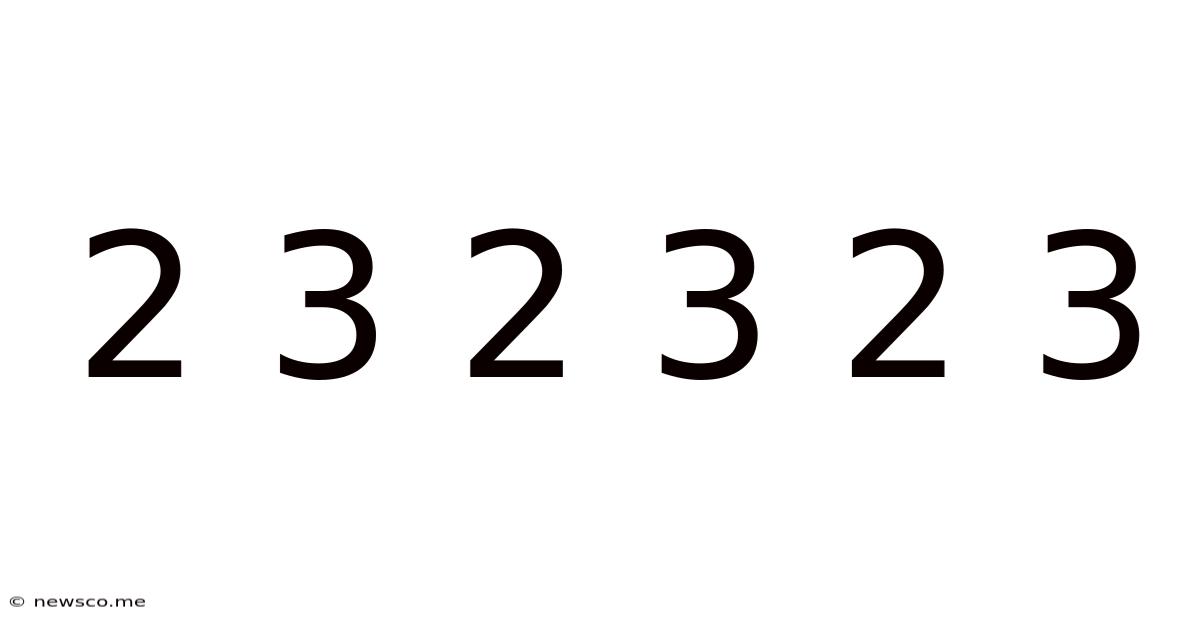
Table of Contents
Decoding the Mysterious Sequence: 2 3 2 3 2 3
The seemingly simple sequence "2 3 2 3 2 3" might appear innocuous at first glance. However, this numerical pattern opens a door to a fascinating exploration of mathematics, music, rhythm, and even potential applications in various fields. This article delves deep into the possibilities this sequence presents, examining its mathematical properties, rhythmic interpretations, potential symbolic meanings, and potential applications beyond the purely numerical.
The Mathematical Perspective: Exploring Patterns and Properties
From a purely mathematical standpoint, "2 3 2 3 2 3" presents an intriguing repeating pattern. Its simplicity belies a potential for deeper analysis. We can explore several avenues:
1. Simple Repetition and Periodicity:
The most obvious observation is the periodicity of the sequence. The sequence repeats itself with a period of two. This inherent regularity makes it straightforward to extrapolate the sequence to any desired length. We can easily predict the next few numbers: 2 3 2 3 2 3 2 3... and so on. This predictable nature is a fundamental characteristic in many mathematical structures.
2. Generating Functions and Series:
While a simple repeating sequence, we can explore the concept of generating functions. Although not strictly necessary for such a straightforward pattern, generating functions are powerful tools in mathematics for analyzing and manipulating sequences. This sequence, though simple, could serve as a basic example in demonstrating the principles of generating functions.
3. Number Theory and Divisibility:
We can examine the sequence through the lens of number theory. While the numbers themselves are small and prime (2 and 3 are the first two prime numbers!), we can explore divisibility rules or investigate the sums or differences of consecutive terms. For instance, the alternating sum (2-3+2-3+2-3...) converges to zero or a small number, depending on the number of terms. This could be expanded upon with more complex mathematical operations.
4. Relationship to Other Mathematical Structures:
Could this sequence be related to other mathematical structures? It's possible to imagine embedding it within larger matrices or sets. For example, imagine a larger sequence built upon this pattern: 2 3 2 3 2 3 4 5 4 5 4 5..., introducing a new repeating sub-sequence. This approach explores the potential of building more complex structures from simple building blocks.
The Rhythmic Interpretation: Exploring Musical and Temporal Patterns
The sequence "2 3 2 3 2 3" transcends its purely numerical interpretation; it readily lends itself to rhythmic interpretations in music and other time-based arts.
1. Musical Rhythms and Meter:
Imagine this sequence representing note durations in music. We could interpret '2' as two eighth notes and '3' as three eighth notes, creating a rhythmic pattern that repeats. This could form the basis of a simple rhythmic motif or ostinato, providing a foundation for a musical piece. Different note values could also be employed, altering the overall feel and character.
2. Dance and Movement:
In choreography or other movement-based arts, the sequence could be used to determine durations or counts of steps or gestures. A '2' could correspond to two quick steps, while a '3' represents three slower, more deliberate movements. This could create interesting patterns and variations in a dance sequence.
3. Temporal Patterns and Sequencing:
Beyond music and dance, this sequence can represent any temporal sequence, such as light flashes, sound pulses, or even actions in a theatrical performance. The pattern provides a framework for creating structured, repetitive temporal events, enabling exploration of dynamic effects through manipulation of the pattern.
Symbolic and Interpretative Potential: Uncovering Hidden Meanings
The sequence "2 3 2 3 2 3" might hold symbolic meaning, depending on the context. While no inherent universal symbolism exists, creative interpretations can be developed:
1. Binary and Ternary Oppositions:
The numbers 2 and 3 could represent fundamental binary and ternary oppositions often found in mythology, philosophy, and other cultural contexts. For example, 2 could symbolize duality (light/dark, good/evil), while 3 could signify the trinity or a three-part structure. The repeated pattern could represent the ongoing interplay between these opposing forces.
2. Cycles and Recurrence:
The repetitive nature of the sequence could symbolize cyclical processes in nature or human life – the continuous ebb and flow, the rise and fall, or the repetition of patterns. This interpretation lends itself to creative explorations of thematic development.
3. Personal and Contextual Meanings:
The meaning of the sequence can be entirely personal. Someone might find significance in it based on personal experiences, associations, or beliefs. This individual approach underscores the versatility of such numerical patterns in symbolic representation.
Potential Applications Beyond the Abstract: Exploring Practical Uses
While "2 3 2 3 2 3" might seem abstract, its predictable nature and inherent rhythm makes it applicable in various fields:
1. Coding and Programming:
In computer science, such simple repeating patterns can serve as examples in teaching or demonstrating fundamental programming concepts, like loops and iterations. The sequence could form the basis for creating simple algorithms or simulations.
2. Signal Processing and Pattern Recognition:
The sequence might serve as a simple test signal in signal processing applications. Its known characteristics make it useful in testing algorithms for pattern recognition or analysis.
3. Robotics and Automation:
The sequence could be used to program simple movements or actions in robotics. A robot arm could be programmed to repeat a sequence of movements based on the numerical pattern.
4. Data Structures and Algorithms:
The sequence's predictable nature makes it ideal for illustrating data structures in computer science. It could serve as a basic example to explain the concepts of arrays, lists, or other data structures that hold sequential information.
Conclusion: Exploring the Depth of Simplicity
The seemingly simple sequence "2 3 2 3 2 3" reveals surprising depth upon closer examination. Its mathematical properties provide a foundation for exploring concepts like periodicity and generating functions. Its rhythmic interpretations open doors to musical composition, choreography, and temporal arts. Furthermore, its symbolic potential allows for creative interpretations across diverse fields, ranging from philosophy to personal symbolism. Finally, its practical applications in computer science, signal processing, and robotics demonstrate its versatility beyond purely abstract considerations. This little sequence shows that even the simplest things can hold remarkable complexity and potential. Its enduring appeal lies in its adaptability and the myriad of ways it can be interpreted and applied across various disciplines. The continued exploration of simple sequences like this fosters creativity and deepens our understanding of the relationship between numbers, rhythm, and symbolism.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 2 3 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.