2 3 2 3 2 3 2 3
News Co
Apr 13, 2025 · 5 min read
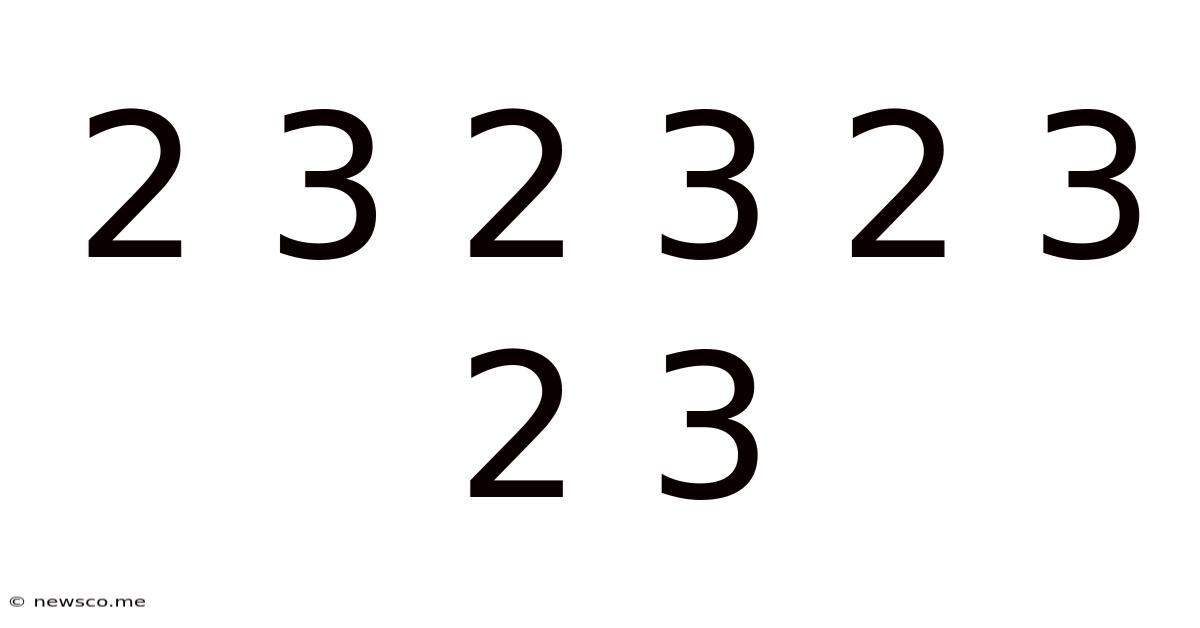
Table of Contents
Decoding the Mysterious Sequence: 2 3 2 3 2 3 2 3
The seemingly simple sequence "2 3 2 3 2 3 2 3" holds a surprising depth of potential interpretations. While at first glance it appears arbitrary, a closer examination reveals possibilities spanning various fields, from mathematics and music to psychology and even cryptography. This article will delve into the numerous ways we can approach this sequence, exploring its possible meanings and the underlying principles that govern our interpretations.
The Mathematical Perspective: Patterns and Sequences
From a purely mathematical standpoint, "2 3 2 3 2 3 2 3" represents a repeating sequence. This immediately suggests several avenues of exploration:
1. Simple Repetition: The most basic interpretation is simply a repeating pattern of "2 3". This is the most obvious and arguably the least insightful interpretation. However, understanding this foundational repetition is crucial before venturing into more complex analyses. It highlights the concept of periodicity and its importance in various mathematical fields.
2. Fibonacci-like Structures? Although not directly a Fibonacci sequence (where each number is the sum of the two preceding ones), we can explore relationships. One could attempt to construct a generative rule based on the alternating nature of 2 and 3. However, a simple, elegant formula connecting the sequence members remains elusive. This exploration leads us to consider more nuanced approaches to pattern recognition.
3. Modular Arithmetic: The sequence could be interpreted through the lens of modular arithmetic. For instance, if we consider the sequence modulo 5 (the remainder after division by 5), we get: 2, 3, 2, 3, 2, 3, 2, 3. This doesn't immediately reveal significant insights, but exploring different moduli could potentially uncover hidden structures. This approach exemplifies the power of algebraic manipulation in uncovering deeper meanings in seemingly simple patterns.
4. Generating Functions: More advanced mathematical tools like generating functions could be employed. These functions represent sequences as power series, allowing for the analysis of their properties and potential generalizations. While applying such tools to this specific sequence might not yield earth-shattering results, the approach highlights the potential of advanced mathematics in tackling such problems.
The Musical Interpretation: Rhythm and Meter
The sequence "2 3 2 3 2 3 2 3" readily lends itself to musical interpretation. We can view the numbers as representing note durations or rhythmic values:
1. Simple Rhythmic Pattern: The simplest interpretation is a rhythmic motif. Imagine "2" representing a half note and "3" representing a dotted quarter note (or vice-versa, depending on the time signature). This would create a repetitive rhythmic figure that could form the basis of a simple melody or accompaniment. This underscores the importance of simple, repeated structures in music.
2. Exploring Meter: The alternating nature of the sequence can inform the meter of a piece of music. It could, for instance, suggest a compound meter like 6/8, where the "2" and "3" correspond to different groupings of eighth notes. This invites experimentation with different time signatures and their influence on the perceived rhythm. Understanding meter and rhythm is crucial in music composition and analysis.
3. Polyrhythms: The sequence could be interpreted as a basis for polyrhythms – multiple rhythmic patterns happening simultaneously. Imagine one instrument playing a "2" rhythm while another plays a "3" rhythm; the interplay would create a rich and complex rhythmic texture. This illustrates the potential for creating sophisticated musical textures from relatively simple starting points.
Psychological and Cognitive Perspectives
The sequence's simplicity belies its potential for psychological and cognitive investigations:
1. Pattern Recognition: The ease or difficulty with which individuals recognize the repetitive nature of the sequence can reveal aspects of their cognitive processing. Studies could explore how factors like age, cognitive abilities, and prior experience influence pattern recognition. This ties into the broader field of cognitive psychology and the study of perception.
2. Predictive Abilities: Presenting the sequence and then interrupting it can test individuals' predictive abilities. For example, presenting "2 3 2 3 2 3 2" and asking for the next number would reveal how well individuals can extrapolate patterns. Such experiments would explore the cognitive mechanisms underlying prediction and pattern extrapolation.
3. Memory and Recall: The repetitive nature of the sequence could be used to study memory and recall. Researchers could investigate how well individuals remember the sequence after different delays or under varying conditions. This could shed light on different memory systems and their limitations.
Cryptographic Possibilities: Simple Cipher or Key?
While unlikely to be a robust cryptographic system, the sequence could theoretically be part of a simple cipher or key:
1. Substitution Cipher: The numbers could represent letters in a simple substitution cipher. For instance, "2" might correspond to "B" and "3" to "C." However, this would be a highly insecure cipher, easily cracked with frequency analysis. This highlights the limitations of simplistic cryptographic systems.
2. Part of a Key: The sequence might represent a portion of a longer key within a more complex encryption algorithm. However, such a short sequence would be extremely vulnerable to brute-force attacks. The exploration of this aspect emphasizes the importance of key length and complexity in secure cryptography.
The broader implications: Abstraction and Representation
Beyond the specific interpretations mentioned above, the sequence "2 3 2 3 2 3 2 3" serves as a microcosm of broader ideas concerning abstraction and representation:
-
Abstraction: The sequence itself is an abstraction; it's a representation of something else. The meaning we assign to it depends entirely on the context and the lens through which we view it. Understanding this emphasizes the importance of contextual understanding.
-
Representation: The diverse interpretations—mathematical, musical, psychological—highlight the multiplicity of ways a simple pattern can be represented and interpreted. This showcases the flexibility of symbolic representation and its role in communication and knowledge construction.
-
The Power of Simplicity: The inherent simplicity of the sequence allows for a wide range of interpretations, highlighting the potential for seemingly simple structures to underly complex phenomena. This encourages a closer look at the seemingly mundane for hidden complexities.
In conclusion, the sequence "2 3 2 3 2 3 2 3," while initially appearing insignificant, offers a fertile ground for exploration across multiple disciplines. Its analysis underscores the multifaceted nature of pattern recognition, the power of different analytical frameworks, and the importance of considering context in interpreting symbolic representations. The seemingly simple can often hold surprising depths, demanding a multifaceted approach to uncover its full potential. This exploration encourages us to view the world with a more curious and inquisitive eye, seeking connections and meanings beyond the readily apparent.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 2 3 2 3 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.