2 3/4 On A Number Line
News Co
May 08, 2025 · 5 min read
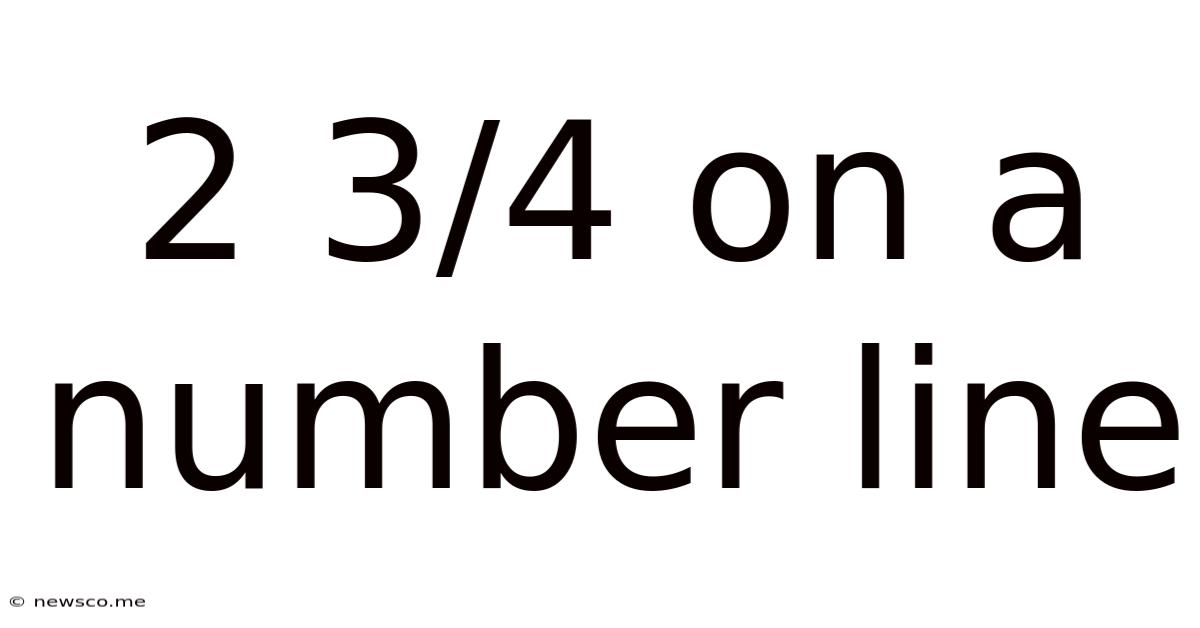
Table of Contents
2 3/4 on a Number Line: A Comprehensive Guide
Understanding fractions and their representation on a number line is a fundamental skill in mathematics. This comprehensive guide delves into the intricacies of placing mixed numbers, specifically 2 3/4, on a number line, exploring various methods and providing a solid foundation for further mathematical exploration. We'll cover the basics, delve into different approaches, and address common misconceptions to ensure a thorough understanding.
Understanding Mixed Numbers and Fractions
Before we tackle placing 2 3/4 on a number line, let's solidify our understanding of mixed numbers and fractions.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. For instance, 2 3/4 means two whole units and three-quarters of another unit. This representation is often more intuitive than using improper fractions (where the numerator is larger than the denominator), like 11/4, which represents the same quantity.
What is a Proper Fraction?
A proper fraction has a numerator (top number) smaller than its denominator (bottom number). In 2 3/4, 3/4 is a proper fraction, indicating a part of a whole.
Converting Mixed Numbers to Improper Fractions:
While mixed numbers are visually intuitive, improper fractions are often easier to work with in certain mathematical operations. To convert 2 3/4 to an improper fraction:
- Multiply the whole number by the denominator: 2 * 4 = 8
- Add the numerator: 8 + 3 = 11
- Keep the same denominator: 11/4
Therefore, 2 3/4 is equivalent to 11/4.
Placing 2 3/4 on a Number Line: Different Approaches
There are several ways to accurately place 2 3/4 on a number line. The best approach depends on the context and the level of precision required.
Method 1: Dividing the Units into Quarters
This is the most straightforward method.
- Draw a Number Line: Draw a number line and label the integers, starting from, say, 0 and extending to at least 3.
- Divide Each Unit: Divide each unit (the space between consecutive integers) into four equal parts. This represents the denominator of our fraction (4).
- Locate 2 3/4: Start at 2 on the number line. Since the fraction is 3/4, count three segments to the right of 2. The point you land on represents 2 3/4.
Method 2: Using Equivalent Fractions
This method is particularly useful when dealing with fractions that are not easily divided into equal parts.
- Find an Equivalent Fraction: You could find an equivalent fraction of 3/4 with a larger denominator to increase the accuracy of placement on the number line. For example, 3/4 is equivalent to 6/8 or 9/12. This will allow for finer divisions on the number line, making the placement of 2 3/4 more precise.
- Divide Accordingly: Divide each unit on your number line into the appropriate number of parts according to the denominator of the equivalent fraction (e.g., 8 parts if using 6/8).
- Locate 2 3/4: Locate the point that corresponds to the numerator of your equivalent fraction starting from 2.
Method 3: Converting to a Decimal
Converting the fraction to a decimal provides another precise way to locate the point on the number line.
- Convert to Decimal: Divide the numerator by the denominator: 3 ÷ 4 = 0.75
- Add the Whole Number: Add the whole number part: 2 + 0.75 = 2.75
- Locate on the Number Line: Locate 2.75 on the number line. This point represents 2 3/4. This method is particularly useful if your number line is already marked with decimal increments.
Understanding the Significance of Number Lines
Number lines are more than just tools for visualizing fractions; they are crucial for understanding several key mathematical concepts:
- Ordering Numbers: Number lines help visualize the order of numbers, showing which numbers are greater or less than others. This is particularly useful when comparing fractions and decimals. Clearly, 2 3/4 is greater than 2 and less than 3.
- Operations with Numbers: Number lines can facilitate understanding of addition and subtraction, visually representing the movement along the line. Adding 1/4 to 2 3/4 on the number line would move you one segment to the right, reaching 3.
- Introducing Negative Numbers: Number lines extend beyond zero into negative values, providing a visual representation of negative numbers and their relationships to positive numbers.
- Decimals and Fractions: Number lines bridge the gap between fractions and decimals, illustrating their equivalence.
Common Misconceptions and How to Avoid Them
Several common misunderstandings can arise when working with fractions and number lines:
- Unequal Divisions: The most common mistake is dividing the units on the number line unevenly. Ensure that each unit is divided into an equal number of parts corresponding to the denominator of the fraction.
- Incorrect Placement: Make sure to accurately count the segments after the whole number. A simple counting error can lead to the wrong placement.
- Misunderstanding Equivalent Fractions: Not correctly identifying equivalent fractions can result in an inaccurate representation on the number line.
Advanced Applications and Further Exploration
The skill of placing fractions like 2 3/4 on a number line is foundational for more advanced mathematical concepts:
- Coordinate Geometry: Understanding number lines is crucial for understanding coordinate systems in two and three dimensions, which are essential for graphing equations and functions.
- Inequalities: Number lines help visualize inequalities involving fractions and mixed numbers.
- Real Number System: Number lines are an integral part of understanding the real number system, which includes all rational and irrational numbers.
Conclusion
Accurately placing 2 3/4 on a number line requires a strong understanding of fractions, mixed numbers, and the principles of dividing a unit into equal parts. By mastering the different methods discussed, including using equivalent fractions and converting to decimals, one can confidently represent this and other fractions on a number line. The ability to visualize fractions on a number line is crucial for developing a comprehensive understanding of numerical concepts and lays a strong foundation for more complex mathematical applications. Remember to pay close attention to detail, ensuring accurate divisions and precise counting when working with number lines to prevent common errors. The practice and understanding discussed will significantly enhance your mathematical abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3/4 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.