2 3 5 7 11 13
News Co
Apr 14, 2025 · 6 min read
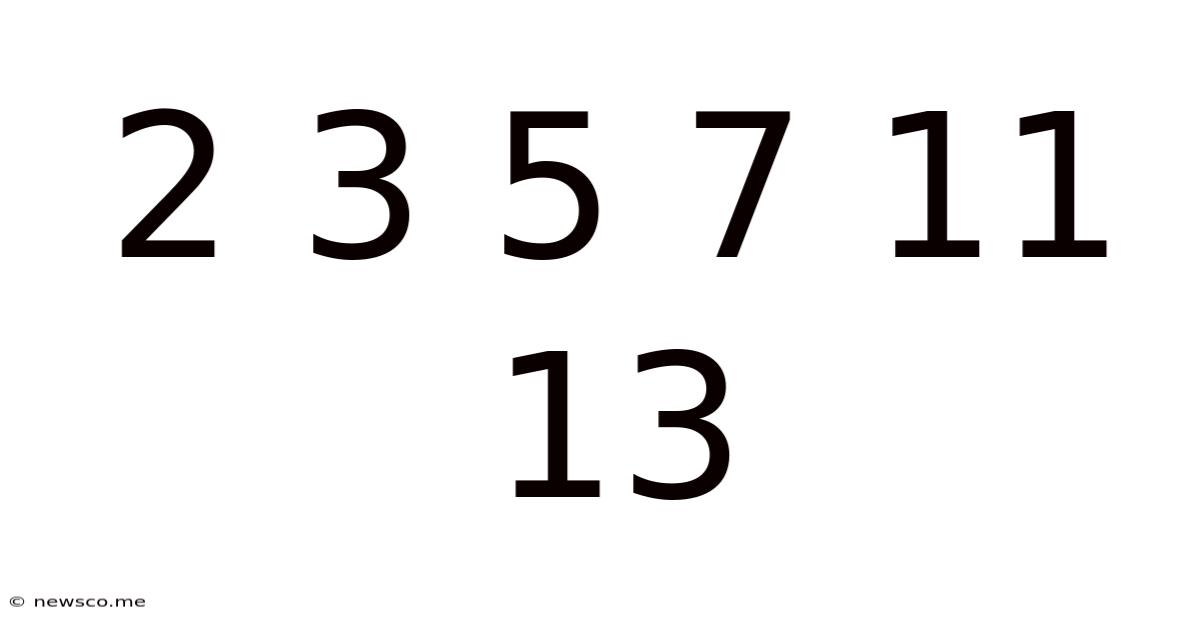
Table of Contents
Decoding the Enigma: Exploring the Sequence 2, 3, 5, 7, 11, 13... and Beyond
The seemingly simple sequence 2, 3, 5, 7, 11, 13… holds a profound mathematical significance, captivating mathematicians and number enthusiasts for centuries. At first glance, it might appear arbitrary, but a closer look reveals a fascinating pattern: these are the prime numbers. This article delves deep into the world of prime numbers, exploring their properties, significance, and the ongoing quest to understand their distribution.
What are Prime Numbers?
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, a prime number is only divisible by 1 and itself. This seemingly simple definition belies the complex and fascinating nature of these numbers. Our initial sequence, 2, 3, 5, 7, 11, and 13, are all prime because they fulfill this condition.
Examples of Prime Numbers:
- 2 is the smallest and only even prime number.
- 3, 5, 7, 11, 13, 17, 19, 23, 29, 31... and so on.
Examples of Non-Prime Numbers (Composite Numbers):
- 4 (2 x 2)
- 6 (2 x 3)
- 8 (2 x 2 x 2)
- 9 (3 x 3)
- 10 (2 x 5)
The Fundamental Theorem of Arithmetic
The importance of prime numbers stems from the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This theorem forms the cornerstone of many areas of number theory and has far-reaching implications in mathematics and computer science. This means that prime numbers are the fundamental building blocks of all integers.
The Distribution of Prime Numbers: An Unpredictable Dance
While we can identify prime numbers, predicting their occurrence is a notoriously difficult problem. There's no simple formula to generate the next prime number. The distribution of prime numbers appears seemingly random, yet mathematicians have discovered intriguing patterns and relationships.
The Prime Number Theorem
One of the most significant breakthroughs in understanding prime distribution is the Prime Number Theorem. It states that the number of primes less than a given number x is approximately x / ln(x), where ln(x) is the natural logarithm of x. While this doesn't give an exact count, it provides an excellent approximation for large values of x.
Gaps Between Prime Numbers
The difference between consecutive prime numbers is called a prime gap. These gaps can vary significantly. Sometimes, primes are clustered closely together, while other times there are large gaps. The study of prime gaps is an active area of research, with mathematicians continually exploring the patterns and limits of these gaps. The twin prime conjecture, which proposes an infinite number of pairs of primes differing by 2 (like 3 and 5, or 11 and 13), is a prominent example of this ongoing investigation.
The Sieve of Eratosthenes: A Timeless Algorithm
One of the oldest and most elegant methods for finding prime numbers is the Sieve of Eratosthenes. This algorithm works by iteratively eliminating multiples of prime numbers, starting from 2. It's a simple yet effective way to identify primes within a given range. While not suitable for finding extremely large primes, its historical significance and simplicity make it a cornerstone of prime number exploration.
Prime Numbers in Cryptography: Securing Our Digital World
Prime numbers play a crucial role in modern cryptography, particularly in public-key cryptography. Algorithms like RSA rely on the difficulty of factoring large numbers into their prime factors. The security of these cryptographic systems depends on the computational infeasibility of factoring the product of two large prime numbers. This makes prime numbers essential for securing online transactions, communication, and data storage.
The Riemann Hypothesis: One of Mathematics' Greatest Unsolved Mysteries
The Riemann Hypothesis, formulated by Bernhard Riemann in 1859, is one of the most important unsolved problems in mathematics. It concerns the distribution of prime numbers and proposes a connection between the zeros of the Riemann zeta function and the distribution of primes. Solving the Riemann Hypothesis would have profound implications for our understanding of prime numbers and number theory in general. Its solution remains elusive, captivating mathematicians and inspiring ongoing research.
Mersenne Primes: Giants in the Prime Number World
Mersenne primes are prime numbers of the form 2<sup>p</sup> - 1, where p is also a prime number. These primes are often extremely large, and the search for new Mersenne primes is an ongoing quest, aided by the Great Internet Mersenne Prime Search (GIMPS), a distributed computing project involving thousands of volunteers. The largest known prime numbers are often Mersenne primes, pushing the boundaries of computational power and our understanding of prime number distribution.
Applications Beyond Cryptography: Prime Numbers in Diverse Fields
The significance of prime numbers extends far beyond cryptography. They appear in various areas, including:
- Coding theory: Prime numbers are used in error-correcting codes, ensuring reliable data transmission.
- Hashing algorithms: Prime numbers are used in hash functions, which are fundamental to data structures and algorithms.
- Random number generation: Prime numbers are employed in algorithms for generating pseudo-random numbers.
- Physics and other sciences: Prime number patterns have been observed in various natural phenomena, though the connection isn't always fully understood.
Ongoing Research and Future Directions
The study of prime numbers is a vibrant and active field of research. Mathematicians continue to explore open problems, including:
- The twin prime conjecture: Proving or disproving the existence of infinitely many twin primes.
- Goldbach's conjecture: Proving that every even integer greater than 2 can be expressed as the sum of two primes.
- Understanding the distribution of prime gaps: Developing more precise models for predicting the spacing between consecutive prime numbers.
- Improving algorithms for finding large primes: Developing faster and more efficient algorithms to discover increasingly larger prime numbers.
Conclusion: A Journey into the Heart of Numbers
The sequence 2, 3, 5, 7, 11, 13… represents a gateway to a profound and beautiful world of mathematics. The seemingly simple definition of prime numbers hides a wealth of complexity and mystery. From the Fundamental Theorem of Arithmetic to the Riemann Hypothesis, prime numbers have captivated mathematicians for centuries and continue to inspire research and exploration today. Their significance extends far beyond theoretical mathematics, influencing fields as diverse as cryptography, computer science, and even potentially physics. The quest to understand prime numbers is an ongoing journey, pushing the boundaries of our mathematical knowledge and shaping our technological landscape. The seemingly simple sequence holds the key to unlocking deeper understanding of the building blocks of numbers, and the journey to understand them remains a fascinating and rewarding one.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.