2 3 5 7 11 13 17
News Co
Mar 30, 2025 · 6 min read
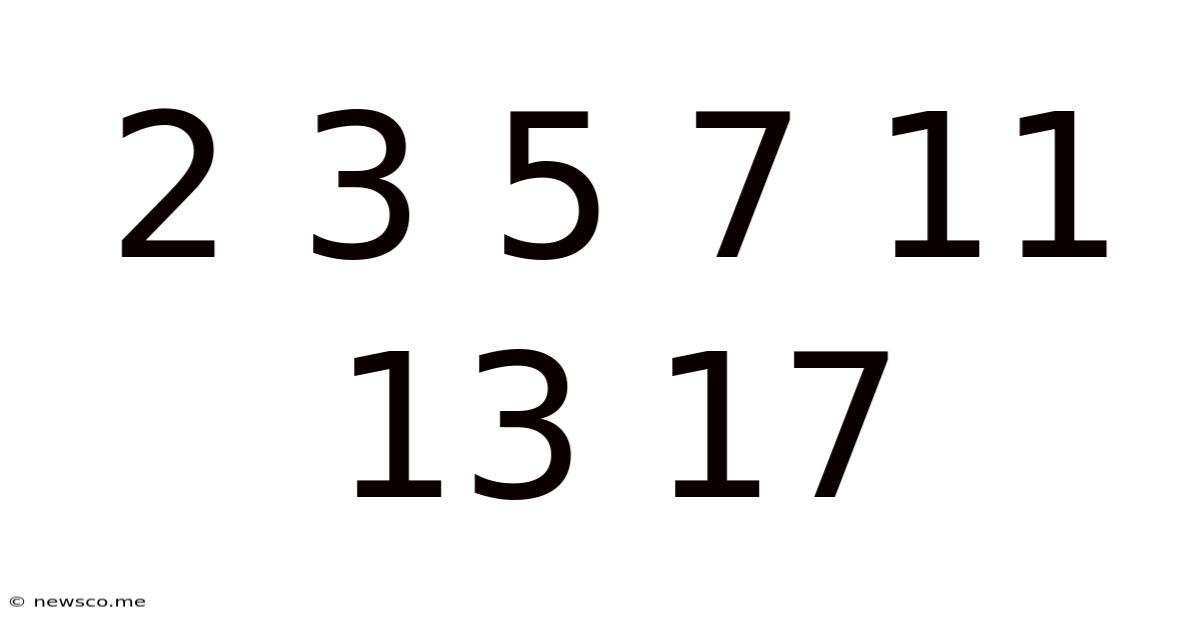
Table of Contents
Decoding the Prime Sequence: 2, 3, 5, 7, 11, 13, 17... and Beyond
The sequence 2, 3, 5, 7, 11, 13, 17… might seem unremarkable at first glance. However, this seemingly simple list represents the foundation of number theory: prime numbers. These numbers, divisible only by 1 and themselves, form the building blocks of all other integers. Understanding their properties, distribution, and the ongoing quest to unravel their mysteries is a journey into the heart of mathematics. This article delves into the fascinating world of prime numbers, exploring their characteristics, historical significance, applications, and the persistent challenges they present to mathematicians worldwide.
What are Prime Numbers?
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and so on. Note that 1 is not considered a prime number. This seemingly simple definition belies the profound complexity hidden within these numbers.
Distinguishing Primes from Composites
The opposite of a prime number is a composite number. A composite number is a positive integer that has at least one divisor other than 1 and itself. For instance, 4 (2 x 2), 6 (2 x 3), and 9 (3 x 3) are all composite numbers. Every integer greater than 1 is either prime or composite.
The Fundamental Theorem of Arithmetic
The importance of prime numbers stems from the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers, disregarding the order of the factors. This theorem underpins much of number theory and has far-reaching consequences in various fields. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). This unique factorization allows for consistent mathematical operations and analysis.
The Distribution of Prime Numbers: An Ongoing Enigma
One of the most compelling aspects of prime numbers is their seemingly unpredictable distribution among integers. While there's an infinite number of primes, their spacing becomes increasingly erratic as you move along the number line. This irregularity has fascinated mathematicians for centuries, leading to the development of various theorems and conjectures aimed at understanding their distribution.
The Prime Number Theorem
The Prime Number Theorem provides an asymptotic estimate for the number of primes less than a given integer. It states that the number of primes less than x is approximately x/ln(x), where ln(x) is the natural logarithm of x. While not providing an exact count, this theorem offers a powerful approximation of prime density.
The Riemann Hypothesis: A Millennium Problem
The Riemann Hypothesis, one of the most important unsolved problems in mathematics, is directly related to the distribution of prime numbers. It concerns the location of the zeros of the Riemann zeta function, a complex function intricately linked to the prime-counting function. A proof of the Riemann Hypothesis would significantly advance our understanding of prime distribution and its implications across various mathematical fields.
Algorithms for Finding Prime Numbers
Throughout history, mathematicians have developed various algorithms to identify prime numbers. These algorithms range from simple trial division to sophisticated probabilistic tests used in cryptography.
Trial Division: A Basic Approach
Trial division is a straightforward method for checking if a number is prime. It involves dividing the number by all integers from 2 up to its square root. If any division results in a whole number, the number is composite; otherwise, it's prime. While effective for smaller numbers, trial division becomes computationally expensive for larger ones.
Sieve of Eratosthenes: A More Efficient Method
The Sieve of Eratosthenes is a significantly more efficient algorithm for finding all prime numbers up to a specified integer. It iteratively marks composite numbers starting with the multiples of 2, then 3, and so on. The numbers that remain unmarked after the process are prime.
Probabilistic Primality Tests: Handling Large Numbers
For very large numbers, probabilistic primality tests, such as the Miller-Rabin test, are employed. These tests don't guarantee primality but provide a high probability of correctness. Their efficiency makes them essential in cryptographic applications where dealing with large prime numbers is crucial.
Applications of Prime Numbers
The seemingly abstract nature of prime numbers belies their crucial role in various practical applications, most notably in cryptography.
Cryptography: Securing Digital Communication
Prime numbers are the cornerstone of many modern cryptographic systems. Algorithms like RSA (Rivest-Shamir-Adleman) rely on the difficulty of factoring large composite numbers into their prime factors. This difficulty forms the basis for secure communication over the internet, protecting sensitive data from unauthorized access.
Hashing and Data Integrity
Prime numbers also play a vital role in hashing algorithms, used for data integrity checks. Hash functions, often incorporating prime numbers, generate unique "fingerprints" for data, allowing for efficient verification of data integrity and detection of tampering.
Coding Theory: Error Correction
Prime numbers are used in coding theory to construct error-correcting codes. These codes enable reliable data transmission over noisy channels by adding redundancy, utilizing the mathematical properties of prime numbers to detect and correct errors.
Open Questions and Ongoing Research
Despite centuries of research, many questions about prime numbers remain unanswered. This ongoing quest for knowledge drives significant research in number theory and related fields.
Twin Primes Conjecture
The Twin Primes Conjecture postulates that there are infinitely many pairs of twin primes – prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). While significant progress has been made, a definitive proof remains elusive.
Goldbach's Conjecture
Goldbach's Conjecture proposes that every even integer greater than 2 can be expressed as the sum of two prime numbers (e.g., 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5). This conjecture has been extensively tested computationally, but a formal proof is still lacking.
The Search for Mersenne Primes
Mersenne primes are prime numbers of the form 2<sup>p</sup> - 1, where p is also a prime number. The Great Internet Mersenne Prime Search (GIMPS) is a distributed computing project dedicated to finding new Mersenne primes, pushing the boundaries of computational power and contributing to our understanding of prime number distribution.
Conclusion: The Enduring Allure of Prime Numbers
The sequence 2, 3, 5, 7, 11, 13, 17… and beyond represents more than just a list of numbers. Prime numbers are fundamental building blocks of mathematics, deeply intertwined with the structure of integers and possessing profound implications across various fields. Their seemingly random distribution, coupled with their crucial role in applications like cryptography, continues to fascinate and challenge mathematicians, ensuring that the quest to unravel their mysteries will persist for generations to come. The ongoing exploration of prime numbers is a testament to the enduring power of mathematical inquiry and its ability to connect seemingly disparate areas of knowledge. From theoretical number theory to practical applications in computer science, the influence of these simple yet enigmatic numbers remains immense and far-reaching.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 13 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.