2 3 5 7 11 13 17 19 23
News Co
Apr 24, 2025 · 6 min read
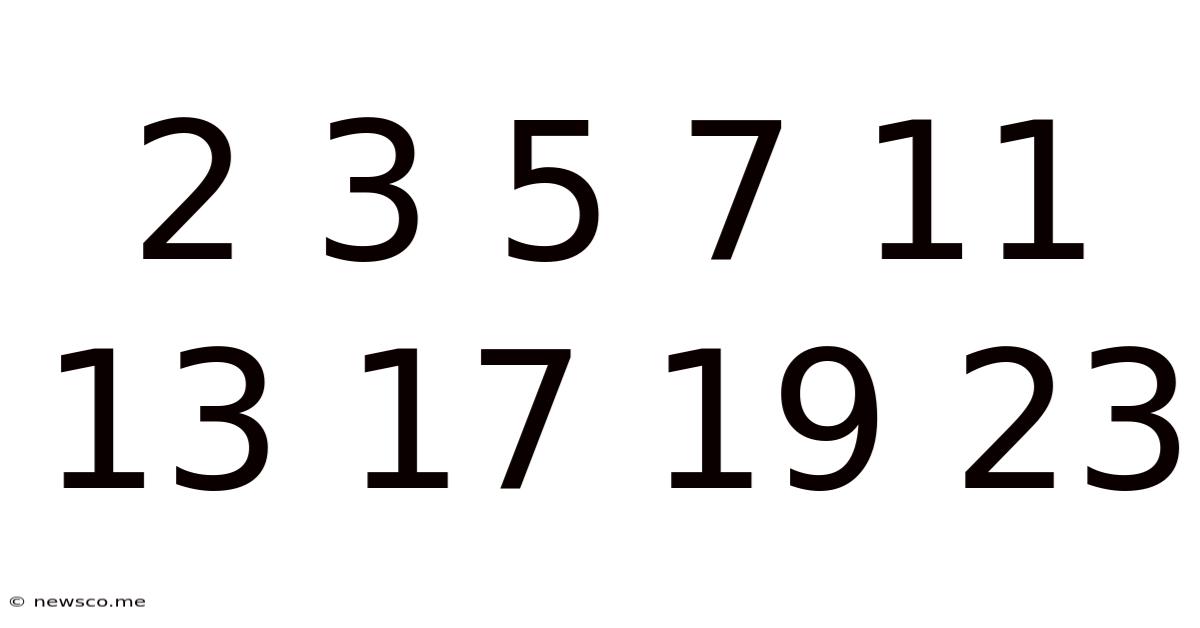
Table of Contents
Unveiling the Secrets of Prime Numbers: Exploring the Sequence 2, 3, 5, 7, 11, 13, 17, 19, 23
The sequence 2, 3, 5, 7, 11, 13, 17, 19, 23 represents the first nine prime numbers. This seemingly simple sequence holds a profound fascination for mathematicians and continues to be a source of ongoing research and exploration. Understanding prime numbers is crucial not only in pure mathematics but also in areas like cryptography and computer science. This article delves deep into the world of prime numbers, focusing on the sequence given, exploring their properties, significance, and the mysteries they still hold.
What are Prime Numbers?
Before we dive into the specifics of our sequence, let's establish a firm understanding of prime numbers themselves. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's a number that can only be divided evenly by 1 and itself. The number 1, while seemingly simple, is not considered a prime number.
The sequence 2, 3, 5, 7, 11, 13, 17, 19, 23 perfectly exemplifies this definition. Each number in the sequence is only divisible by 1 and itself. This seemingly simple characteristic is the foundation for many complex mathematical concepts.
The Significance of the First Nine Primes
The first nine primes – 2, 3, 5, 7, 11, 13, 17, 19, 23 – are foundational building blocks within number theory. Their properties and relationships underpin many mathematical theorems and algorithms. Let's explore some key aspects:
2: The Only Even Prime Number
The number 2 stands out as the only even prime number. This unique characteristic stems directly from the definition of a prime number. Any even number greater than 2 can be divided by 2, making it composite (not prime). This peculiarity of 2 has important implications in various mathematical proofs and algorithms.
Distribution and the Prime Number Theorem
The spacing between prime numbers isn't uniform. Sometimes they cluster relatively close together, while other times there are larger gaps. This irregular distribution is a central theme in number theory. The Prime Number Theorem, a cornerstone of analytic number theory, provides an approximation of the distribution of prime numbers. While it doesn't give the exact location of each prime, it offers a probabilistic understanding of their density as numbers grow larger. The theorem states that the number of primes less than or equal to a given number x is approximately x / ln(x), where ln(x) is the natural logarithm of x. This theorem helps us understand the asymptotic behavior of primes, even if it doesn't predict their exact locations.
Prime Factorization and the Fundamental Theorem of Arithmetic
Every composite number can be uniquely expressed as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic. This theorem is crucial for many aspects of number theory and has practical applications in cryptography. For example, the security of RSA encryption relies heavily on the difficulty of factoring large composite numbers into their prime factors. Consider the number 15. Its prime factorization is 3 x 5. This unique factorization is fundamental to our understanding of number systems.
Exploring the Sequence: Patterns and Properties
While there's no immediately obvious pattern in the sequence 2, 3, 5, 7, 11, 13, 17, 19, 23 beyond their primality, let's delve into some properties and explore potential avenues of investigation:
Consecutive Primes and Gaps
Analyzing the gaps between consecutive primes in this sequence reveals varying distances. The gap between 2 and 3 is 1, between 3 and 5 is 2, between 5 and 7 is 2, and so on. The irregular spacing between prime numbers is a topic of ongoing mathematical research. Understanding the distribution of these gaps is a significant challenge. The largest gap within our sequence is 4 (between 13 and 17). The study of prime gaps provides valuable insights into the overall distribution of primes.
Twin Primes: A Glimpse into Deeper Mysteries
Twin primes are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 5 and 7, 11 and 13). Our sequence contains one pair of twin primes: 3 and 5, and another potential pair 11 and 13. Whether infinitely many twin primes exist is one of the most famous unsolved problems in number theory, known as the Twin Prime Conjecture. While not proven, significant progress has been made in recent years, suggesting a strong likelihood of its truth. The study of twin primes and other prime constellations provides a rich area for exploration.
Prime Number Spirals: Visualizing Distribution
Visual representations like Ulam Spirals provide interesting visualizations of the distribution of prime numbers. Although not directly related to our specific sequence, Ulam spirals illustrate the non-random nature of prime number distribution, showcasing patterns and clusters that emerge within the seemingly chaotic arrangement. Such visualizations aid in our understanding of prime number distribution and stimulate further investigation.
The Importance of Prime Numbers in Cryptography
The inherent properties of prime numbers play a critical role in modern cryptography, particularly in the field of public-key cryptography. The difficulty of factoring large composite numbers into their prime factors forms the basis of security for many widely used encryption algorithms, such as RSA (Rivest-Shamir-Adleman). The larger the prime numbers used, the more secure the encryption becomes. This makes the ongoing research into prime numbers crucial for maintaining the security of digital communication and data.
Prime Numbers in Computer Science
Beyond cryptography, prime numbers find applications in various areas of computer science. Hash functions, used for data integrity and security, often utilize prime numbers in their algorithms. Random number generators, crucial for simulations and other computational tasks, sometimes leverage properties of prime numbers to ensure better randomness. The study and application of prime numbers in computer science continues to evolve as technology progresses.
Conclusion: The Enduring Enigma of Primes
The sequence 2, 3, 5, 7, 11, 13, 17, 19, 23, representing the first nine prime numbers, serves as a gateway to the fascinating and challenging world of prime number theory. While seemingly simple at first glance, the distribution, properties, and applications of prime numbers continue to captivate mathematicians and computer scientists alike. From the fundamental theorem of arithmetic to the security of modern cryptography, prime numbers are essential elements of mathematics and technology. The ongoing research into prime numbers, particularly into unsolved problems like the Twin Prime Conjecture and the Riemann Hypothesis, promises to unveil further mysteries and deepen our understanding of these fundamental building blocks of numbers. The study of prime numbers remains a vibrant and active field, continuously pushing the boundaries of mathematical knowledge and driving innovation in technology. The simple sequence at the beginning of this exploration underscores the vast and complex world that unfolds from the study of prime numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 13 17 19 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.