2 3 5 7 11 13 17 19 23 29
News Co
May 08, 2025 · 5 min read
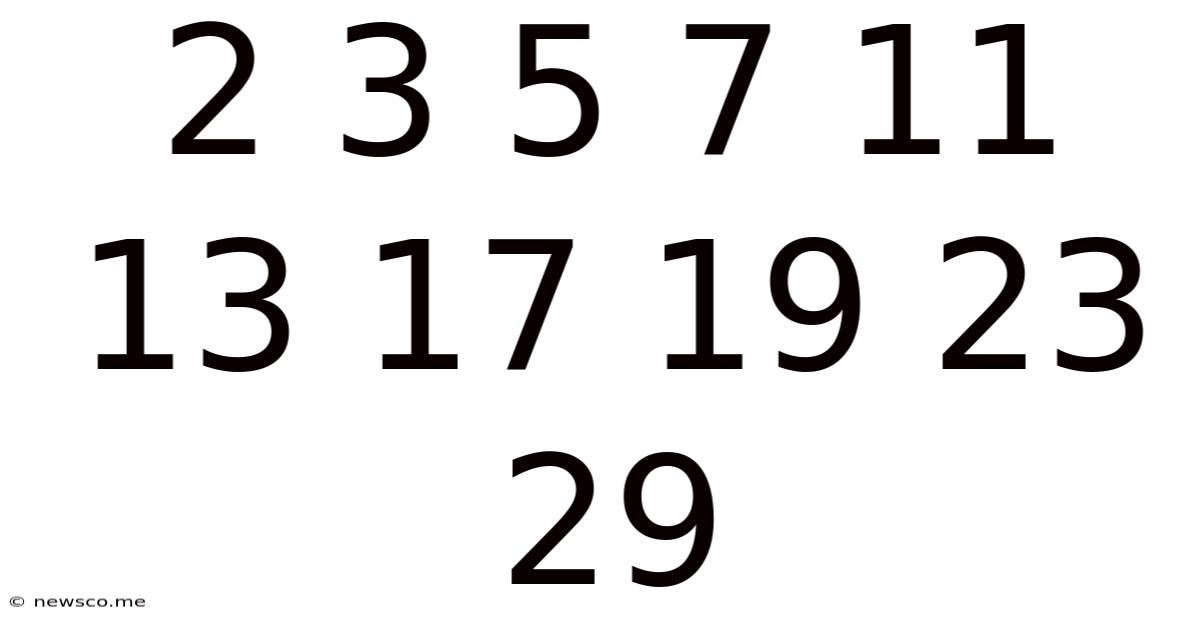
Table of Contents
The Enchanting World of Prime Numbers: Unveiling the Mysteries of 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29
The sequence 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29 might seem unremarkable at first glance. However, these ten numbers represent the very essence of number theory: they are the first ten prime numbers. Prime numbers, the building blocks of all integers, hold a captivating allure for mathematicians and enthusiasts alike, their inherent mystery driving centuries of research and exploration. This article delves deep into the world of prime numbers, focusing on this particular sequence and exploring their properties, significance, and the ongoing quest to understand their distribution.
What are Prime Numbers?
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, it's a number divisible only by 1 and itself. Our sequence – 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 – perfectly illustrates this definition. Each number in the sequence is only divisible by 1 and itself.
The Fundamental Theorem of Arithmetic
The significance of prime numbers stems from the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This is akin to prime numbers being the fundamental "atoms" of arithmetic. Consider the number 12. It can be factored as 2 x 2 x 3, a unique combination of prime numbers. This theorem underpins many crucial concepts in number theory and algebra.
Exploring the First Ten Primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29
Let's examine some interesting properties of these first ten primes:
2: The Only Even Prime
2 holds a unique position as the only even prime number. All other even numbers are divisible by 2, making them composite (non-prime). This singularity makes 2 an exceptionally important prime in many mathematical contexts.
3, 5, 7: The First Few Odd Primes
3, 5, and 7 are the next three primes in our sequence, highlighting that prime numbers can be both even and odd, though after 2, all subsequent primes are odd.
Twin Primes: 3 and 5, 17 and 19
Twin primes are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 17 and 19). These pairs are fascinating because their occurrence seems somewhat random, posing challenges to their prediction and distribution. The search for twin primes and understanding their distribution is an active area of research.
Prime Gaps: The Spaces Between Primes
The gaps between consecutive prime numbers are not uniform. For instance, the gap between 3 and 5 is 2, while the gap between 17 and 19 is also 2, but the gap between 23 and 29 is 6. The study of prime gaps provides insights into the erratic yet structured distribution of primes.
Prime Number Theorem: Predicting the Distribution
The Prime Number Theorem is a landmark result that provides an approximation for the distribution of prime numbers. It states that the number of primes less than a given number x is approximately x/ln(x), where ln(x) is the natural logarithm of x. While this theorem doesn’t provide an exact formula, it offers a powerful tool for estimating the density of primes.
The Significance of Prime Numbers
The significance of prime numbers extends far beyond the realm of pure mathematics. Their properties and patterns have found applications in various fields:
Cryptography: The Cornerstone of Secure Communication
Cryptography, the science of secure communication, relies heavily on the properties of prime numbers. Algorithms like RSA encryption utilize the difficulty of factoring large composite numbers into their prime factors to ensure secure data transmission. This is why the discovery of new, large prime numbers remains crucial for maintaining the security of digital communications.
Computer Science: Algorithms and Data Structures
Prime numbers play a role in efficient algorithms and data structures used in computer science. Hash tables, for example, often employ prime numbers to minimize collisions and optimize performance.
Coding Theory: Error Detection and Correction
Coding theory, focused on error detection and correction in data transmission, often utilizes prime numbers in the design of error-correcting codes. The structure and properties of primes help to develop robust codes capable of detecting and correcting errors during data transmission.
The Ongoing Search for Primes: Mersenne Primes and Beyond
The search for prime numbers continues to be a fascinating and challenging endeavor. Specific types of primes, such as Mersenne primes (primes of the form 2<sup>p</sup> - 1, where 'p' is also a prime number), have received significant attention due to their unique properties and association with the Great Internet Mersenne Prime Search (GIMPS) project.
The search for ever-larger prime numbers helps to test the limits of computational power and algorithms. Furthermore, the study of large primes contributes to our understanding of prime number distribution and related mathematical conjectures.
The Riemann Hypothesis: A Millennium Problem
One of the most significant unsolved problems in mathematics is the Riemann Hypothesis, which concerns the distribution of prime numbers. This hypothesis, if proven, would have profound implications for our understanding of prime number distribution and related mathematical areas. The Riemann Hypothesis remains one of the Clay Mathematics Institute's Millennium Prize Problems, offering a significant reward for its solution.
Conclusion: The Enduring Mystery of Primes
The sequence 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29, while seemingly simple, represents a gateway into the rich and complex world of prime numbers. These fundamental building blocks of arithmetic have fascinated mathematicians for centuries, driving research and exploration in number theory, cryptography, computer science, and beyond. The seemingly random distribution of primes, the pursuit of ever-larger primes, and the challenge of solving problems like the Riemann Hypothesis continue to captivate the mathematical community and underscore the enduring mystery and importance of prime numbers. Their study not only expands our mathematical knowledge but also fuels advancements in crucial fields such as secure communication and data processing. The journey of discovery surrounding prime numbers is far from over, promising even more exciting revelations in the years to come.
Latest Posts
Latest Posts
-
Formula For The Height Of A Trapezoid
May 09, 2025
-
Derivative Of A Log Base 2
May 09, 2025
-
What Is The Value Of Y Units Units Units Units
May 09, 2025
-
Find X And Y In Each Figure
May 09, 2025
-
Find The Perimeter Of An Equilateral Triangle
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2 3 5 7 11 13 17 19 23 29 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.