2/3 Divided By 1/3 In Fraction
News Co
May 08, 2025 · 5 min read
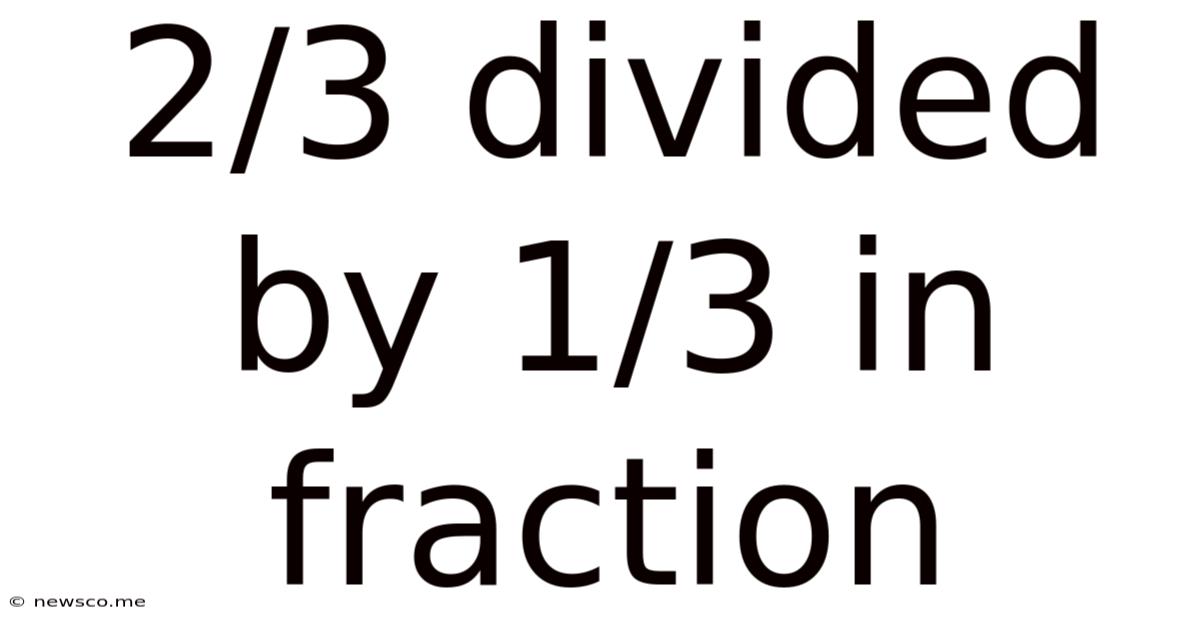
Table of Contents
2/3 Divided by 1/3: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process and a few helpful strategies, it becomes straightforward. This article will explore the division of 2/3 by 1/3 in detail, providing a comprehensive explanation suitable for various levels of mathematical understanding. We'll go beyond just finding the answer and delve into the underlying principles, exploring different methods and offering practical applications.
Understanding Fraction Division
Before tackling our specific problem (2/3 ÷ 1/3), let's establish a firm foundation in fraction division. The core concept involves understanding what division means. When we divide a number by another, we're essentially asking: "How many times does the second number fit into the first?" This same logic applies to fractions.
The "Keep, Change, Flip" Method (Reciprocal Method)
The most common method for dividing fractions is the "keep, change, flip" method, also known as the reciprocal method. This method streamlines the process and avoids the complexities of complex fractions.
- Keep: Keep the first fraction exactly as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (find its reciprocal). The reciprocal of a fraction is simply the fraction turned upside down; the numerator becomes the denominator and vice versa.
Let's illustrate with a simple example: 1/2 ÷ 1/4.
- Keep: 1/2
- Change: ×
- Flip: 4/1 (reciprocal of 1/4)
The problem now becomes 1/2 × 4/1 = 4/2 = 2. Therefore, 1/4 fits into 1/2 two times.
The Common Denominator Method
While the "keep, change, flip" method is generally preferred for its simplicity, understanding the common denominator method provides a deeper insight into the underlying principles of fraction division.
This method involves converting both fractions to equivalent fractions with a common denominator. Once the denominators are the same, the division becomes a simple division of the numerators.
Let's revisit our simple example: 1/2 ÷ 1/4.
- Find a Common Denominator: The least common denominator of 2 and 4 is 4.
- Convert to Equivalent Fractions: 1/2 becomes 2/4.
- Divide the Numerators: 2/4 ÷ 1/4 = 2 ÷ 1 = 2.
This method clearly shows that we are asking how many times 1/4 fits into 2/4.
Solving 2/3 Divided by 1/3
Now, let's apply our knowledge to the problem at hand: 2/3 ÷ 1/3.
Using the "Keep, Change, Flip" Method
- Keep: 2/3
- Change: ×
- Flip: 3/1 (reciprocal of 1/3)
This gives us: 2/3 × 3/1 = (2 × 3) / (3 × 1) = 6/3 = 2.
Therefore, 1/3 fits into 2/3 two times.
Using the Common Denominator Method
Both fractions already have a common denominator of 3. Therefore, we can directly divide the numerators:
2/3 ÷ 1/3 = 2 ÷ 1 = 2.
This again confirms our answer: 1/3 fits into 2/3 two times.
Visualizing Fraction Division
Visual aids can significantly improve understanding, especially for those who find abstract mathematical concepts challenging. Imagine you have a pizza cut into three equal slices. 2/3 represents two of those slices. If each slice (1/3) is considered a unit, how many of those units (slices) do you have? You have two. This visual representation perfectly mirrors our mathematical result.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous real-world applications. Consider these examples:
- Cooking: A recipe calls for 2/3 cup of flour, but you only want to make 1/3 of the recipe. You would need to divide 2/3 by 3 (or multiply by 1/3) to find the amount of flour needed.
- Sewing: You have 2/3 of a yard of fabric and need to cut it into pieces that are 1/3 of a yard each. Fraction division helps determine how many pieces you can cut.
- Construction: A project requires 2/3 of a ton of gravel, and you have bags that each contain 1/3 of a ton. Dividing 2/3 by 1/3 tells you how many bags you need.
Advanced Concepts and Extensions
While our primary focus has been on 2/3 ÷ 1/3, let's briefly explore more complex scenarios involving fraction division:
- Dividing Fractions with Mixed Numbers: Mixed numbers (like 1 1/2) need to be converted into improper fractions before applying the "keep, change, flip" or common denominator method. For example, 1 1/2 ÷ 1/3 becomes 3/2 ÷ 1/3.
- Dividing Fractions with Unlike Denominators: The common denominator method becomes crucial when dealing with fractions that don't share a common denominator. Finding the least common denominator simplifies the process.
- Complex Fractions: Complex fractions have fractions within fractions. These are solved by simplifying the numerator and denominator separately before performing the division.
Conclusion
Mastering fraction division opens doors to a deeper understanding of mathematics and its practical applications. The "keep, change, flip" method offers a straightforward approach, while the common denominator method provides a deeper conceptual understanding. By understanding both methods, and by visualizing the process, students can confidently tackle a wide array of fraction division problems, from simple calculations to more complex scenarios. Remember, practice is key to mastering any mathematical concept. The more you work with fractions, the more intuitive and comfortable the process will become. So, grab a pencil and paper, and keep practicing! You'll be amazed at how quickly your skills improve. Remember to explore different methods and find the one that best suits your learning style. And don't be afraid to ask for help when needed! Mathematical understanding is a journey, not a race.
Latest Posts
Latest Posts
-
Find The Area Of The Following Composite Figure
May 09, 2025
-
Rounding To The Nearest Hundred Worksheet
May 09, 2025
-
What Is 30 Of 25 Dollars
May 09, 2025
-
What Are The Greatest Common Factors Of 75
May 09, 2025
-
Write The Following As An Exponential Expression
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Divided By 1/3 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.